SKEDSOFT

State Spaces: One general formulation of intelligent action is in terms of state space. A state contains all of the information necessary to predict the effects of an action and to determine if it is a goal state. State-space searching assumes that

• the agent has perfect knowledge of the state space and can observe what state it is in (i.e., there is full observability);
• the agent has a set of actions that have known deterministic effects;

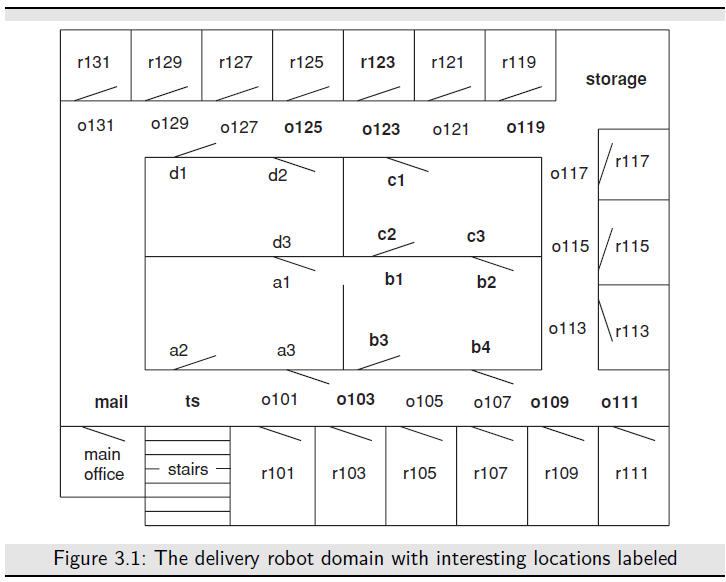
• some states are goal states, the agent wants to reach one of these goal states, and the agent can recognize a goal state; and
• a solution is a sequence of actions that will get the agent from its current state to a goal state.

A state-space problem consists of

• a set of states;
• a distinguished set of states called the start states;
• a set of actions available to the agent in each state;
• an action function that, given a state and an action, returns a new state;
• a set of goal states, often specified as a Boolean function, goal(s), that is true when s is a goal state; and
• a criterion that specifies the quality of an acceptable solution. For example, any sequence of actions that gets the agent to the goal state may be acceptable, or there may be costs associated with actions and the agent may be required to find a sequence that has minimal total cost. This is called an optimal solution. Alternatively, it may be satisfied with any solution that is within 10% of optimal.

This framework is extended in subsequent chapters to include cases where an agent can exploit the internal features of the states, where the state is not  fully observable (e.g., the robot does not know where the parcels are, or the teacher does not know the aptitude of the student), where the actions are stochastic (e.g., the robot may overshoot, or the student perhaps does not learn a topic that is taught), and where complex preferences exist in terms of rewards and punishments, not just goal states.