SKEDSOFT
A Pumping Lemma for CFLs: Consider any CFG G = (N, Σ,P,S). A Pumping Lemma for the language of this grammar, L(G), can be derived by noting that a “very long string” w ∈ L(G) requires a very long derivation sequence to derive it from S. Since we only have a finite number of non-terminals, some non-terminal must repeat in this derivation sequence, and furthermore, the second occurrence of the non-terminal must be a result of expanding the first occurrence (it must lie within the parse tree generated by the first occurrence). For example, consider the CFG
S -> (S) |T| e
T -> [T] |T T| e.
Here is an example derivation:
S => ( S ) => ((T)) => (( [T] )) => (( [ ] ))
Occurrence-1 Occurrence-2
Occurrence-1 involves Derivation-1: T => [ T ] => [ ]
Occurrence-2 involves Derivation-2: T => e
Here, the second T arises because we took T and expanded it into [ T ] and then to [ ]. Now, the basic idea is that we can use Derivation-1 used in the first occurrence in place of Derivation-2, to obtain a longer string:
S => (S) => ((T)) => (( [ T ] )) => (( [[ T ]] )) => (( [[ ]] ))
^ ^
Occurrence-1 Use Derivation-1 here
In the same fashion, we can use Derivation-2 in place of Derivation-1 to obtain a shorter string, as well:
S => ( S ) => ( ( T ) ) => ( ( ) )
^
Use Derivation-2 here
When all this happens, we can find a repeating non-terminal that can be pumped up or down. In our present example, it is clear that we can manifest (([i ]i)) for i ≥ 0 by either applying Derivation-2 directly, or by applying some number of Derivation-1s followed by Derivation-2. In order to conveniently capture the conditions mentioned so far, it is good to resort to parse trees. Consider a CFG with |V | non-terminals, and with the right-hand side of each rule containing at most b syntactic elements (terminals or non-terminals). Consider a b-ary tree built up to height |V | 1, as shown in Figure 13.7. The string yielded on the frontier of the tree w = uvxyz. If there are two such parse trees for w, pick the one that has the fewest number of nodes. Now, if we avoid having the same non-terminal used in any path from the root to a leaf, basically each path will “enjoy” a growth up to height at most |V | (recall that the leaves are terminals). The string w = uvxyz is, in this case, of length at most b|V |. This implies that if we force the string to be of length b|V | 1 (called p hereafter), a parse tree for this string will have some path that repeats a non-terminal. Call the higher occurrence V1 and the lower occurrence (contained within V1) V2. Pick the lowest two such repeating pair of non-terminals. Now, we have these facts:
- |vxy| ≤ p; if not, we would find two other non-terminals that exist lower in the parse tree than V1 and V2, thus violating the fact that V1 and V2 are the lowest two such.
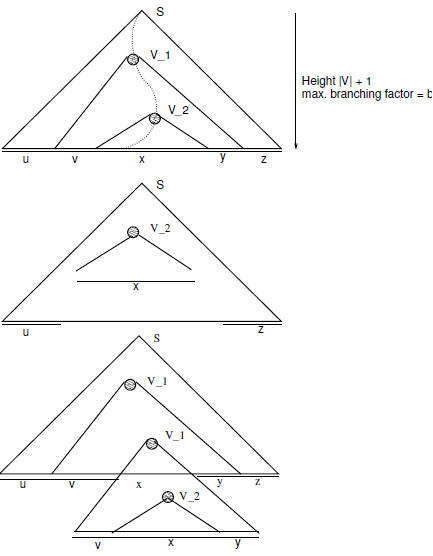
Fig. 13.7. Depiction of a parse tree for the CFL Pumping Lemma. The upper drawing shows a very long path that repeats a non-terminal, with the lowest two repetitions occurring at V 2 and V 1 (similar to Occurrence-1 and Occurrence-2 as in the text). With respect to this drawing: (i) the middle drawing indicates what happens if the derivation for V 2 is applied in lieu of that of V 1, and (ii) the bottom drawing depicts what happens if the derivation for V 2 is replaced by that for V 1, which, in turn, contains a derivation for V 2
- |vx| ≥ 1; if not, we will in fact have w = uxz, for which a shorter parse tree exists (namely, the one where we directly employ V2).
- Now, by pumping, we can obtain the desired repetitions of v and y, as described in Theorem 13.1.
Theorem 13.1. Given any CFG G = (N, Σ,P,S), there exists a number p such that given a string w in L(G) such that |w| ≥ p, we can split w into w = uvxyz such that |vy| > 0, |vxy| ≤ p, and for every i ≥ 0, uvixyiz ∈ L(G).
We can apply this Pumping Lemma for CFGs in the same manner as we did for regular sets. For example, let us sketch that Lww of page 230 is not context-free.
Illustration 13.8.1 Suppose Lww were a CFL. Then the CFL Pumping Lemma would apply. Let p be the pumping length associated with a CFG of this language. Consider the string 0p1p0p1p which is in Lww. The segments v and y of the Pumping Lemma are contained within the first 0p1p block, in the middle 1p0p block or in the last 0p1p block, and in each of these cases, it could also have fallen entirely within a 0p block or a 1p block. By pumping up or down, we will then obtain a string that is not within Lww.