SKEDSOFT
CONTEXT SENSITIVE GRAMMARS AND LANGUAGES: A context-sensitive Language is a language generated by a context sensitive grammar.
Definition 1: A context-sensitive grammar is one whose productions are all of the form
xAy-> xvy
where AÎv and x, v, y ∈ (V ÈT )* .
“Context-sensitive” implies the fact that the actual string modification is given by A-> v, while the x and y provide the context in which the rule may be applied.
Definition 2: A context-sensitive grammar is one whose productions are all of the form
x-> y
where x, y∈ (V ÈT ) , and | x| £| y|.
This type of grammar is called “Non-contracting” as the derivation steps never decrease the length of the sentential form.
This definition given above is mostly used. The two kinds of grammar are almost equivalent generating the same languages with only the exception: One kind of grammar permits languages to contain the empty string, while the other doesn’t. A language L is context-sensitive if there exists a context sensitive grammar G such that either L = L(G) or L = L(G)È{l}
Example 1: Show that the language L = {a nbncn | n ≥1} is a context-sensitive language.
Solution: Let us prove this by showing a context-sensitive grammar for the language.

This uses the variables A and B. Since the language is not context-free, it is said to be context-sensitive language.
LINEAR BOUNDED AUTOMATA: A Turing machine has an infinite supply of blank tape. A linear-bounded automaton is a Turing machine whose tape is only an squares long, where ‘n’ is the length of the input string and a is a constant associated with the particular linear-bounded automaton.
THEOREM (I): For every context-sensitive language L there exists a linear-bounded automaton M such that L = L(M), i.e. M accept exactly the strings of L.
THEO REM (II): For every language L accepted by a linear-bounded automaton that produces exactly L or L - {l}, depending on the definition of context sensitive grammar.
RELATIONSHIP OF OTHER GRAMMARS
THE O REM (I): Every context-free language is context-sensitive.
Proof: The productions of a context-free language have the form A-> v. The productions of a context-sensitive language have the form xAy-> xvy, where x
and y are permitted to be l. Hence the result.
THE O REM (II): There exists a context-sensitive language that is not context-free.
Proof: The language {a nbncn | n ≥ 0} is not context-free (which could be proved using a pumping lemma). It can be shown that it is context-sensitive by providing an appropriate grammar. The productions of one such grammar is given here.
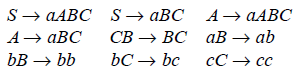
THEOREM (III): Every context-sensitive language is recursive.
Proof: A context-sensitive grammar is non-contracting. Moreover, for any integer n there are only a finite number of sentential forms of length n. Therefore, for any string w we could set a bound on the number of derivation steps required to generate w, hence a bound on the number of possible derivations. The string w is in the language if and only if one of these derivations produces w.