SKEDSOFT

FORMAL SYSTEMS: The necessary properties of a satisfactory formal system are as follows:

(a) Completeness: It should be possible either to prove or disprove any proposition that can be expressed in the system.

(b) Consistency: It should not be possible to both prove and disprove a proposition in the system.

Consistency becomes crucial if it becomes possible to prove and disprove some proposition in the system, which means the same can be done for every proposition in the system. In the late 1800’s there were a lot of mathematicians who were working on a method of putting together all of mathematics, starting from the axions of set theory.

In fact, sets can have other sets as members. In 1901 Bertrand Russel discovered the Russel’s Paradox:

Russel’s Paradox: “Consider the set of all sets that do not have themselves as a member. Is this set a member of itself?”

This problem was tried to be resolved by the way of defining “type”. This theory of types though not accepted fully has paved way for new philosophies of mathematics.

Godel was able to express proofs as numbers like considering a computer program to be a very large binary number. Godel proved the following result:

• “If it is possible to prove, within a formal system, that the system is consistent, then the formal system is not, in fact, consistent.” Equivalently, we can say,
• “If a formal system is consistent, then it is impossible to prove (within the system) that it is consistent.”

This particular result shows that any attempt to prove mathematics consistent is foredoomed to failure. It is still possible to prove a system consistent by logical arguments outside that system, provided the outer system is known to be consistent.

RECURSIVE FUNCTION THEORY: It is seen that a sufficiently powerful formal system cannot be both consistent and complete as proved by Godel. Simple arithmetic on integers is an example of a system that is “sufficiently powerful”. It is always preferred to give up completeness rather than consistency, because in a consistent system any proposition can be proven.

Ideally, we wanted to have an algorithmic theorem proving procedure to distinguish between the provable propositions and unprovable ones. Alan Turing invented Turing machines in an attempt to solve this problem. With the halting problem, Alan Turing had shown that it is not possible to distinguish between soluable and insolvable problems. Similar results were arrived at by other scientists. Church invented “Recursive Function Theory”.

PRIMITIVE RECURSIVE FUNCTIONS: This section describes the basic ideas behind recursive function theory. The Recursive functions are described over the natural numbers I = {0, 1, 2, 3, ......}. Recursive functions are looked at as “Pure Symbol Systems”.

Numbers are not used in the system, rather, we use the system to construct both numbers and arithmetical functions on numbers. Its a different numbering system, in the same way as Roman numerals are different. The correspondence is as given below.

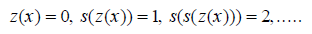
In order to translate to decimal, just count the number of s’s surrounding the central z(x).

(a)    Zero Function: z(x)= z( y), for all x, yÎI . This is our “zero”; it is written as a function so we don’t have to introduce constants into the system.

(b)    Successor Function s(x): This function informally means x 1. Formally, it does not return a value. It just lies there, the result of s(x) is s(x).

(c)    Projector Function:

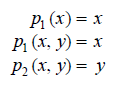
These projector functions are a way of extracting one of the parameters and discarding the rest. We define only P1 and P2 as only functions of no more than two arguments are only discused.

Definition:A total function f over N is primitive recursive if (i) it is any one of the three initial functions [zero function, successor function and Projector Function] or (ii) it can be got by applying composition and recursion finite number of times to the set of initial functions. This is dealt with in the subsequent sections.

Example 1: How are the following functions defined.

(a) Zero function Z(x)

(b) Successor function S(x)

(c) Projection function Pi xn ( ).

Solution

(a) Zero function Z(x) = 0

(b) Successor function S(x) = x 1

(c) Projection function