SKEDSOFT

Mechanical system:

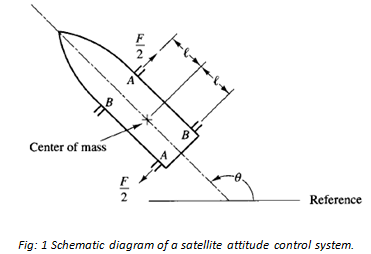
Consider the satellite attitude control system shown in Figure 1. The diagram shows the control of only the yaw angle e. (In the actual system there are controls about three axes.) Small jets apply reaction forces to rotate the satellite body into the desired attitude. The two skew symmetrically placed jets denoted by A or B operate in pairs. Assume that each jet thrust is F/2 and a torque T = Fl is applied to the system. The jets are applied for a certain time duration and thus the torque can be written as T(t). The moment of inertia about the axis of rotation at the center of mass is J.

Let us obtain the transfer function of this system by assuming that torque T(t) is the input, and the angular displacement θ(t) of the satellite is the output.

To derive the transfer function, we proceed according to the following steps.

1. Write the differential equation for the system.

2. Take the Laplace transform of the differential equation, assuming all initial conditions are zero.

3. Take the ratio of the output 8(s) to the input T(s). This ratio is the transfer function.

Applying Newton's second law to the present system and noting that there is no friction in the environment of the satellite, we have

Taking the Laplace transform of both sides of this last equation and assuming all initial conditions to be zero yields

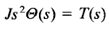
Convolution integral:

For a linear, time-invariant system the transfer function G(s) is

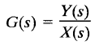
where X(s) is the Laplace transform of the input and Yes) is the Laplace transform of the output, where we assume that all initial conditions involved are zero. It follows that the output yes) can be written as the product of G(s) and X(s), or                                      Y(s) = G(s)X(s)

Note that multiplication in the complex domain is equivalent to convolution in the time domain, so the inverse Laplace transform of Equation above is given by the following convolution integral:

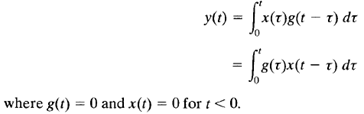
Impulse-response function:

 Consider the output (response) of a system to a unit-impulse input when the initial conditions are zero. Since the Laplace transform of the unit-impulse function is unity, the Laplace transform of the output of the system is

                           Y(s) = G(s)

The inverse Laplace transform of the output given by Equation above gives the impulse response of the system. The inverse Laplace transform of G(s), or

is called the impulse-response function. This function get) is also called the weighting function of the system. The impulse-response function g(t) is thus the response of a linear system to a unit impulse input when the initial conditions are zero. The Laplace transform of this function gives the transfer function. Therefore, the transfer function and impulse-response function of a linear, time-invariant system contain the same information about the system dynamics. It is hence possible to obtain complete information about the dynamic characteristics of the system by exciting it with an impulse input and measuring the response.