SKEDSOFT
This running time can be expressed as an b for constants a and b that depend on the statement costs ci ; it is thus a linear function of n.
If the array is in reverse sorted order-that is, in decreasing order-the worst case results. We must compare each element A[j] with each element in the entire sorted subarray A[1 ‥j - 1], and so tj = j for j = 2, 3, . . . , n. Noting that
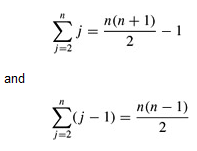
we find that in the worst case, the running time of INSERTION-SORT is
This worst-case running time can be expressed as an2 bn c for constants a, b, and c that again depend on the statement costs ci ; it is thus a quadratic function of n.
Typically, as in insertion sort, the running time of an algorithm is fixed for a given input, although in later chapters we shall see some interesting "randomized" algorithms whose behavior can vary even for a fixed input.
Worst-case and average-case analysis
In our analysis of insertion sort, we looked at both the best case, in which the input array was already sorted, and the worst case, in which the input array was reverse sorted. For the remainder of this book, though, we shall usually concentrate on finding only the worst-case running time, that is, the longest running time for any input of size n. We give three reasons for this orientation.
- The worst-case running time of an algorithm is an upper bound on the running time for any input. Knowing it gives us a guarantee that the algorithm will never take any longer. We need not make some educated guess about the running time and hope that it never gets much worse.
- For some algorithms, the worst case occurs fairly often. For example, in searching a database for a particular piece of information, the searching algorithm's worst case will often occur when the information is not present in the database. In some searching applications, searches for absent information may be frequent.
- The "average case" is often roughly as bad as the worst case. Suppose that we randomly choose n numbers and apply insertion sort. How long does it take to determine where in sub array A[1 ‥ j - 1] to insert element A[j]? On average, half the elements in A[1 ‥ j - 1] are less than A[j], and half the elements are greater. On average, therefore, we check half of the sub array A[1 ‥ j - 1], so tj = j/2. If we work out the resulting average-case running time, it turns out to be a quadratic function of the input size, just like the worst-case running time.