SKEDSOFT

which is the estimated number of atoms in the observable universe.

We define the inverse of the function A_k (n), for integer n ≥ 0, by

α(n) = min {k : A_k(1) = n} .

In words, α(n) is the lowest level k for which A_k(1) is at least n. From the above values of A_k(1), we see that

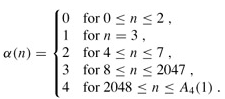
It is only for impractically large values of n (greater than A₄(1), a huge number) that α(n) > 4, and so α(n) ≤ 4 for all practical purposes.

Properties of ranks

In the remainder of this section, we prove an O(m α(n)) bound on the running time of the disjoint-set operations with union by rank and path compression. In order to prove this bound, we first prove some simple properties of ranks.

Proving the time bound

We shall use the potential method of amortized analysis to prove the O(mα(n)) time bound. In performing the amortized analysis, it is convenient to assume that we invoke the LINK operation rather than the UNION operation. That is, since the parameters of the LINK procedure are pointers to two roots, we assume that the appropriate FIND-SET operations are performed separately. The following lemma shows that even if we count the extra FIND-SET operations induced by UNION calls, the asymptotic running time remains unchanged.

In the remainder of this section, we shall assume that the initial sequence of m' MAKE-SET, UNION, and FIND-SET operations has been converted to a sequence of m MAKE-SET, LINK, and FIND-SET operations. We now prove an O(m α(n)) time bound for the converted sequence and appeal to Lemma 21.7 to prove the O(m' α(n)) running time of the original sequence of m' operations.