SKEDSOFT
We need to show that this loop invariant is true prior to the first iteration, that each iteration of the loop maintains the invariant, and that the invariant provides a useful property to show correctness when the loop terminates.
- Initialization:Prior to the first iteration of the loop, i = p - 1, and j = p. There are no values between p and i, and no values between i 1 and j - 1, so the first two conditions of the loop invariant are trivially satisfied. The assignment in line 1 satisfies the third condition.
- Maintenance:As Figure 7.3 shows, there are two cases to consider, depending on the outcome of the test in line 4. Figure 7.3(a) shows what happens when A[j] > x; the only action in the loop is to increment j. After j is incremented, condition 2 holds for A[j - 1] and all other entries remain unchanged. Figure 7.3(b) shows what happens when A[j] ≤ x; i is incremented, A[i] and A[j] are swapped, and then j is incremented. Because of the swap, we now have that A[i] ≤ x, and condition 1 is satisfied. Similarly, we also have that A[j - 1] > x, since the item that was swapped into A[j - 1] is, by the loop invariant, greater than x.
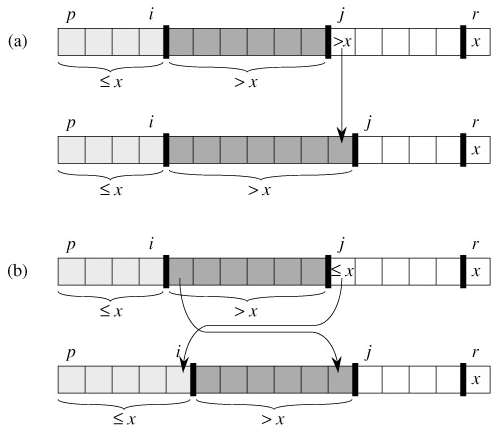
- Figure 7.3: The two cases for one iteration of procedure PARTITION. (a) If A[j] >x, the only action is to increment j, which maintains the loop invariant. (b) If A[j] ≤x, index i is incremented, A[i] and A[j] are swapped, and then j is incremented. Again, the loop invariant is maintained.
- Termination: At termination, j = r. Therefore, every entry in the array is in one of the three sets described by the invariant, and we have partitioned the values in the array into three sets: those less than or equal to x, those greater than x, and a singleton set containing x.
The final two lines of PARTITION move the pivot element into its place in the middle of the array by swapping it with the leftmost element that is greater than x.
The output of PARTITION now satisfies the specifications given for the divide step.
The running time of PARTITION on the subarray A[p ‥ r] is Θ(n), where n = r - p 1