SKEDSOFT
Determining whether any pair of segments intersects
This section presents an algorithm for determining whether any two line segments in a set of segments intersect. The algorithm uses a technique known as "sweeping," which is common to many computational-geometry algorithms. Moreover, as the exercises at the end of this section show, this algorithm, or simple variations of it, can be used to solve other computational-geometry problems.
The algorithm runs in O(n lg n) time, where n is the number of segments we are given. It determines only whether or not any intersection exists; it does not print all the intersections.
In sweeping, an imaginary vertical sweep line passes through the given set of geometric objects, usually from left to right. The spatial dimension that the sweep line moves across, in this case the x-dimension, is treated as a dimension of time. Sweeping provides a method for ordering geometric objects, usually by placing them into a dynamic data structure, and for taking advantage of relationships among them. The line-segment-intersection algorithm in this section considers all the line-segment endpoints in left-to-right order and checks for an intersection each time it encounters an endpoint.
To describe and prove correct our algorithm for determining whether any two of n line segments intersect, we shall make two simplifying assumptions. First, we assume that no input segment is vertical. Second, we assume that no three input segments intersect at a single point. Exercises 33.2-8 and 33.2-9 ask you to show that the algorithm is robust enough that it needs only a slight modification to work even when these assumptions do not hold. Indeed, removing such simplifying assumptions and dealing with boundary conditions is often the most difficult part of programming computational-geometry algorithms and proving their correctness.
Ordering segments
Since we assume that there are no vertical segments, any input segment that intersects a given vertical sweep line intersects it at a single point. Thus, we can order the segments that intersect a vertical sweep line according to the y-coordinates of the points of intersection.
To be more precise, consider two segments s1 and s2. We say that these segments are comparable at x if the vertical sweep line with x-coordinate x intersects both of them. We say that s1 is above s2 at x, written s1 >x s2, if s1 and s2 are comparable at x and the intersection of s1 with the sweep line at x is higher than the intersection of s2 with the same sweep line. In Figure 33.4(a), for example, we have the relationships a >r c, a >t b, b >t c, a >t c, and b >u c. Segment d is not comparable with any other segment.
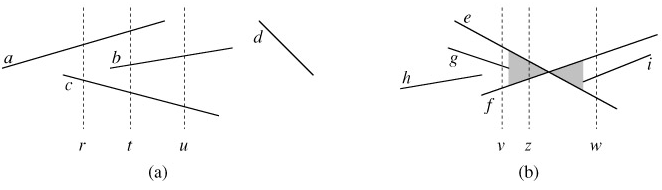
For any given x, the relation ">x" is a total order on segments that intersect the sweep line at x. The order may differ for differing values of x, however, as segments enter and leave the ordering. A segment enters the ordering when its left endpoint is encountered by the sweep, and it leaves the ordering when its right endpoint is encountered.
What happens when the sweep line passes through the intersection of two segments? As Figure 33.4(b) shows, their positions in the total order are reversed. Sweep lines v and w are to the left and right, respectively, of the point of intersection of segments e and f, and we have e >v f and f >w e. Note that because we assume that no three segments intersect at the same point, there must be some vertical sweep line x for which intersecting segments e and f are consecutive in the total order >x. Any sweep line that passes through the shaded region of Figure 33.4(b), such as z, has e and f consecutive in its total order.
Moving the sweep line
Sweeping algorithms typically manage two sets of data:
-
The sweep-line status gives the relationships among the objects intersected by the sweep line.
-
The event-point schedule is a sequence of x-coordinates, ordered from left to right, that defines the halting positions of the sweep line. We call each such halting position an event point. Changes to the sweep-line status occur only at event points.
For some algorithms, the event-point schedule is determined dynamically as the algorithm progresses. The algorithm at hand, however, determines the event points statically, based solely on simple properties of the input data. In particular, each segment endpoint is an event point. We sort the segment endpoints by increasing x-coordinate and proceed from left to right. (If two or more endpoints are covertical, i.e., they have the same x-coordinate, we break the tie by putting all the covertical left endpoints before the covertical right endpoints. Within a set of covertical left endpoints, we put those with lower y-coordinates first, and do the same within a set of covertical right endpoints.) We insert a segment into the sweep-line status when its left endpoint is encountered, and we delete it from the sweep-line status when its right endpoint is encountered. Whenever two segments first become consecutive in the total order, we check whether they intersect.