SKEDSOFT
Indicator random variables: In order to analyze many algorithms, including the hiring problem, we will use indicator random variables. Indicator random variables provide a convenient method for converting between probabilities and expectations. Suppose we are given a sample space S and an event A. Then the indicator random variable I {A} associated with event A is defined as
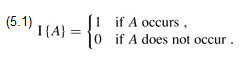
As a simple example, let us determine the expected number of heads that we obtain when flipping a fair coin. Our sample space is S = {H, T}, and we define a random variable Y which takes on the values H and T, each with probability 1/2. We can then define an indicator random variable XH, associated with the coin coming up heads, which we can express as the event Y = H. This variable counts the number of heads obtained in this flip, and it is 1 if the coin comes up heads and 0 otherwise. We write
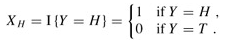
The expected number of heads obtained in one flip of the coin is simply the expected value of our indicator variable XH:
|
E[XH] |
= |
E[I{Y = H}] |
|
|
= |
1 · Pr{Y = H} 0 · Pr{Y = T} |
|
|
= |
1 · (1/2) 0 · (1/2) |
|
|
= |
1/2. |
Thus the expected number of heads obtained by one flip of a fair coin is 1/2. As the following lemma shows, the expected value of an indicator random variable associated with an event A is equal to the probability that A occurs.
Lemma 5.1
Given a sample space S and an event A in the sample space S, let XA = I{A}. Then E[XA] = Pr{A}.
ProofBy the definition of an indicator random variable from equation 1) and the definition of expected value, we have
|
E[XA] |
= |
E[I{A}] |
|
|
= |
1 · Pr{A} 0 · Pr{Ā} |
|
|
= |
Pr{A}, |
where Ā denotes S - A, the complement of A.
Although indicator random variables may seem cumbersome for an application such as counting the expected number of heads on a flip of a single coin, they are useful for analyzing situations in which we perform repeated random trials. In this equation, we compute the number of heads in n coin flips by considering separately the probability of obtaining 0 heads, 1 heads, 2 heads, etc. Making this argument more explicit, we can let Xi be the indicator random variable associated with the event in which the ith flip comes up heads. Letting Yi be the random variable denoting the outcome of the ith flip, we have that Xi = I{Yi = H}. Let X be the random variable denoting the total number of heads in the n coin flips, so that
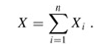
We wish to compute the expected number of heads, so we take the expectation of both sides of the above equation to obtain