SKEDSOFT
Interval Trees: In this section, we shall augment red-black trees to support operations on dynamic sets of intervals. A closed interval is an ordered pair of real numbers [t1, t2], with t1 ≤ t2. The interval [t1, t2] represents the set {t ∈ R : t1 ≤ t ≤ t2}. Open and half-open intervals omit both or one of the endpoints from the set, respectively. In this section, we shall assume that intervals are closed; extending the results to open and half-open intervals is conceptually straightforward.
Intervals are convenient for representing events that each occupy a continuous period of time. We might, for example, wish to query a database of time intervals to find out what events occurred during a given interval. The data structure in this section provides an efficient means for maintaining such an interval database.
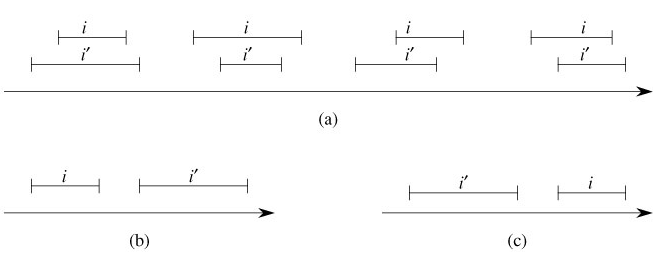
We can represent an interval [t1, t2] as an object i, with fields low[i] = t1 (the low endpoint) and high[i] = t2(the high endpoint). We say that intervals i and i' overlap if i ∩ i' ≠ ø, that is, if low[i] ≤ high[i'] and low[i'] ≤ high[i]. Any two intervals i and i' satisfy the interval trichotomy; that is, exactly one of the following three properties holds:
-
i and i' overlap,
-
i is to the left of i' (i.e., high[i]< low[i']),
-
i is to the right of i' (i.e., high[i']< low[i]).
Figure 14.3 shows the three possibilities.
An interval tree is a red-black tree that maintains a dynamic set of elements, with each element x containing an interval int[x]. Interval trees support the following operations.
-
INTERVAL-INSERT(T, x) adds the element x, whose int field is assumed to contain an interval, to the interval tree T.
-
INTERVAL-DELETE(T, x) removes the element x from the interval tree T.
-
INTERVAL-SEARCH(T, i) returns a pointer to an element x in the interval tree T such that int[x] overlaps interval i, or the sentinel nil[T] if no such element is in the set.
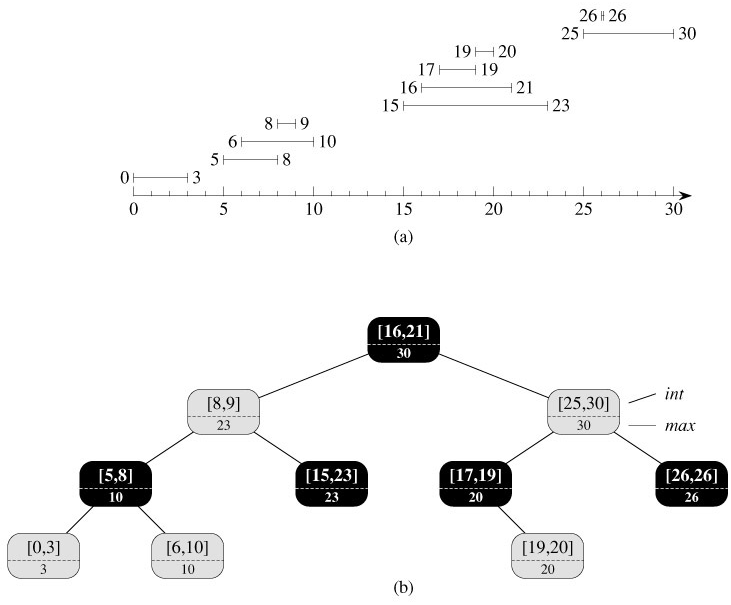
Figure 14.4 shows how an interval tree represents a set of intervals. We shall track the four-step method from Section 14.2 as we review the design of an interval tree and the operations that run on it.
Step 1: Underlying Data Structure
We choose a red-black tree in which each node x contains an interval int[x] and the key of x is the low endpoint, low[int[x]], of the interval. Thus, an inorder tree walk of the data structure lists the intervals in sorted order by low endpoint.
Step 2: Additional Information
In addition to the intervals themselves, each node x contains a value max[x], which is the maximum value of any interval endpoint stored in the subtree rooted at x.
Step 3: Maintaining the Information
We must verify that insertion and deletion can be performed in O(lg n) time on an interval tree of n nodes. We can determine max[x] given interval int[x] and the max values of node x's children:
max[x] = max(high[int[x]], max[left[x]], max[right[x]]).
Step 4: Developing New Operations
The only new operation we need is INTERVAL-SEARCH(T, i), which finds a node in tree T whose interval overlaps interval i. If there is no interval that overlaps i in the tree, a pointer to the sentinel nil[T] is returned.
INTERVAL-SEARCH(T, i) 1 x ← root[T] 2 while x ≠ nil[T] and i does not overlap int[x] 3 do if left[x] ≠ nil[T] and max[left[x]] ≥ low[i] 4 then x ← left[x] 5 else x ← right[x] 6 return x
The search for an interval that overlaps i starts with x at the root of the tree and proceeds downward. It terminates when either an overlapping interval is found or x points to the sentinel nil[T]. Since each iteration of the basic loop takes O(1) time, and since the height of an n-node red-black tree is O(lg n), the INTERVAL-SEARCH procedure takes O(lg n) time.