SKEDSOFT
NP-complete problems: NP-complete problems arise in diverse domains: boolean logic, graphs, arithmetic, network design, sets and partitions, storage and retrieval, sequencing and scheduling, mathematical programming, algebra and number theory, games and puzzles, automata and language theory, program optimization, biology, chemistry, physics, and more. In this section, we shall use the reduction methodology to provide NP-completeness proofs for a variety of problems drawn from graph theory and set partitioning.
Figure 34.13 outlines the structure of the NP-completeness proofs in this section and NP-completeness proofs. Each language in the figure is proved NP-complete by reduction from the language that points to it. At the root is CIRCUIT-SAT,
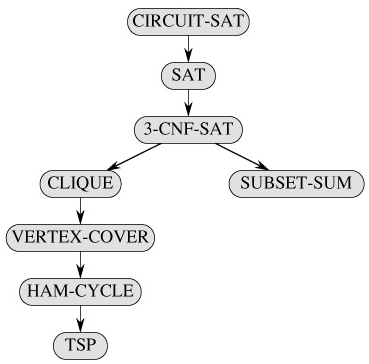
Figure 34.13: The structure of NP-completeness proofs in Sections 34.4 and 34.5. All proofs ultimately follow by reduction from the NP-completeness of CIRCUIT-SAT.
The clique problem: A clique in an undirected graph G = (V, E) is a subset V' ⊆ V of vertices, each pair of which is connected by an edge in E. In other words, a clique is a complete subgraph of G. The size of a clique is the number of vertices it contains. The clique problem is the optimization problem of finding a clique of maximum size in a graph. As a decision problem, we ask simply whether a clique of a given size k exists in the graph. The formal definition is
CLIQUE = {〈G, k〉 : G is a graph with a clique of size k}.
A naive algorithm for determining whether a graph G = (V, E) with |V| vertices has a clique of size k is to list all k-subsets of V , and check each one to see whether it forms a clique. The running time of this algorithm is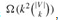 
, which is polynomial if k is a constant. In general, however, k could be near |V| /2, in which case the algorithm runs in superpolynomial time. As one might suspect, an efficient algorithm for the clique problem is unlikely to exist. k
Theorem 34.11: The clique problem is NP-complete.
Proof To show that CLIQUE NP, for a given graph G = (V, E), we use the set V' ⊆ V of vertices in the clique as a certificate for G. Checking whether V' is a clique can be accomplished in polynomial time by checking whether, for each pair u, v ∈ V', the edge (u, v) belongs to E.
We next prove that 3-CNF-SAT ≤P CLIQUE, which shows that the clique problem is NP-hard. That we should be able to prove this result is somewhat surprising, since on the surface logical formulas seem to have little to do with graphs.
The reduction algorithm begins with an instance of 3-CNF-SAT. Let φ = C1 ∧ C2 ∧ ··· ∧ Ck be a boolean formula in 3-CNF with k clauses. For r = 1, 2,..., k, each clause Cr has exactly three distinct literals ,
. We shall construct a graph G such that φ is satisfiable if and only if G has a clique of size k.
The graph G = (V, E) is constructed as follows. For each clause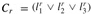 
in φ, we place a triple of vertices ,
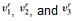into V. We put an edge between two vertices 
if both of the following hold:
-
and are in different triples, that is, r ≠ s, and
-
their corresponding literals are consistent, that is,
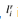is not the negation of 
.
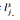This graph can easily be computed from φ in polynomial time. As an example of this construction, if we have
φ = (x1 ∨ ¬x2 ∨ ¬x3) ∧ (¬x1 ∨ x2 ∨ x3) ∧ (x1 ∨ x2 ∨ x3),
then G is the graph shown in Figure 34.14.
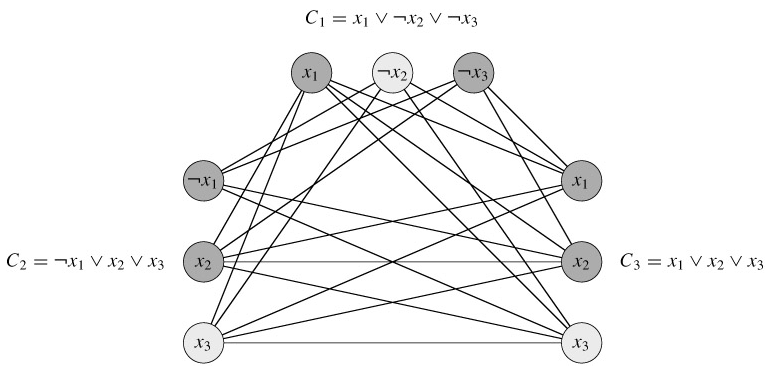
We must show that this transformation of φ into G is a reduction. First, suppose that φ has a satisfying assignment. Then each clause Cr contains at least one literal 
that is assigned 1, and each such literal corresponds to a vertex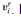 
. Picking one such "true" literal from each clause yields a set V' of k vertices. We claim that V' is a clique. For any two vertices 
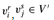, where r ≠ s, both corresponding literals i'i and i'j are mapped to 1 by the given satisfying assignment, and thus the literals cannot be complements. Thus, by the construction of G, the edge 
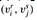belongs to E.
Conversely, suppose that G has a clique V' of size k. No edges in G connect vertices in the same triple, and so V' contains exactly one vertex per triple. We can assign 1 to each literal i'j such that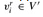 
without fear of assigning 1 to both a literal and its complement, since G contains no edges between inconsistent literals. Each clause is satisfied, and so φ is satisfied. (Any variables that do not correspond to a vertex in the clique may be set arbitrarily.)
