SKEDSOFT

Design Analysis Of Algorithm

Quadratic probing

Quadratic probing uses a hash function of the form

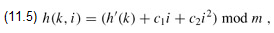
where h' is an auxiliary hash function, c1 and c2 ≠ 0 are auxiliary constants, and i = 0, 1, ..., m - 1. The initial position probed is T[h'(k)]; later positions probed are offset by amounts that depend in a quadratic manner on the probe number i. This method works much better than linear probing, but to make full use of the hash table, the values of c1, c2, and m are constrained. Also, if two keys have the same initial probe position, then their probe sequences are the same, since h(k1, 0) = h(k2, 0) implies h(k1, i) = h(k2, i). This property leads to a milder form of clustering, called secondary clustering. As in linear probing, the initial probe determines the entire sequence, so only m distinct probe sequences are used.

Double hashing

Double hashing is one of the best methods available for open addressing because the permutations produced have many of the characteristics of randomly chosen permutations. Double hashing uses a hash function of the form

h(k, i) = (h1(k) ih2(k)) mod m,

where h1 and h2 are auxiliary hash functions. The initial probe is to position T[h1(k)]; successive probe positions are offset from previous positions by the amount h2(k), modulo m. Thus, unlike the case of linear or quadratic probing, the probe sequence here depends in two ways upon the key k, since the initial probe position, the offset, or both, may vary. Figure 11.5 gives an example of insertion by double hashing.

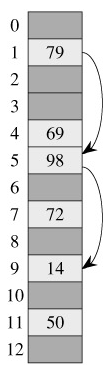
Figure 11.5: Insertion by double hashing. Here we have a hash table of size 13 with h1(k) = k mod 13 and h2(k) = 1 (k mod 11). Since 14 ≡ 1 (mod 13) and 14 ≡ 3 (mod 11), the key 14 is inserted into empty slot 9, after slots 1 and 5 are examined and found to be occupied.

The value h2(k) must be relatively prime to the hash-table size m for the entire hash table to be searched. A convenient way to ensure this condition is to let m be a power of 2 and to design h2 so that it always produces an odd number. Another way is to let m be prime and to design h2 so that it always returns a positive integer less than m. For example, we could choose m prime and let

h1(k)

=

k mod m,

h2(k)

=

1 (k mod m'),

where m' is chosen to be slightly less than m (say, m - 1). For example, if k = 123456, m = 701, and m' = 700, we have h1(k) = 80 and h2(k) = 257, so the first probe is to position 80, and then every 257th slot (modulo m) is examined until the key is found or every slot is examined.

Double hashing improves over linear or quadratic probing in that Θ(m2) probe sequences are used, rather than Θ(m), since each possible (h1(k), h2(k)) pair yields a distinct probe sequence. As a result, the performance of double hashing appears to be very close to the performance of the "ideal" scheme of uniform hashing.

 

Analysis of open-address hashing

Our analysis of open addressing, like our analysis of chaining, is expressed in terms of the load factor α = n/m of the hash table, as n and m go to infinity. Of course, with open addressing, we have at most one element per slot, and thus n ≤ m, which implies α ≤ 1.

We assume that uniform hashing is used. In this idealized scheme, the probe sequence 〈h(k, 0), h(k, 1), ..., h(k, m - 1)〉 used to insert or search for each key k is equally likely to be any permutation of 〈0, 1, ..., m - 1〉. Of course, a given key has a unique fixed probe sequence associated with it; what is meant here is that, considering the probability distribution on the space of keys and the operation of the hash function on the keys, each possible probe sequence is equally likely.

We now analyze the expected number of probes for hashing with open addressing under the assumption of uniform hashing, beginning with an analysis of the number of probes made in an unsuccessful search.