SKEDSOFT
In order to apply equation, we rely on Xk and T(max(k - 1, n - k)) being independent random variables. Exercise 9.2-2 asks you to justify this assertion.
Let us consider the expression max(k - 1, n - k). We have
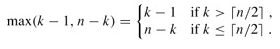
If n is even, each term from T(⌈n/2⌉) up to T(n - 1) appears exactly twice in the summation, and if n is odd, all these terms appear twice and T(⌊n/2⌋) appears once. Thus, we have
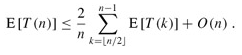
We solve the recurrence by substitution. Assume that T(n) ≤ cn for some constant c that satisfies the initial conditions of the recurrence. We assume that T(n) = O(1) for n less than some constant; we shall pick this constant later. We also pick a constant a such that the function described by the O(n) term above (which describes the non-recursive component of the running time of the algorithm) is bounded from above by an for all n > 0. Using this inductive hypothesis, we have
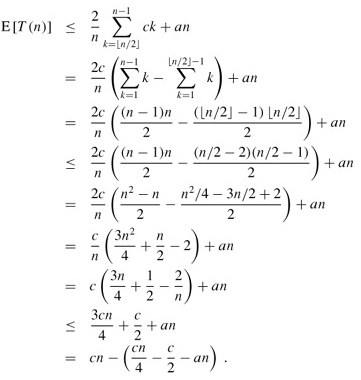
In order to complete the proof, we need to show that for sufficiently large n, this last expression is at most cn or, equivalently, that cn/4 - c/2 - an ≥ 0. If we add c/2 to both sides and factor out n, we get n(c/4 - a) ≥ c/2. As long as we choose the constant c so that c/4 - a > 0, i.e., c > 4a, we can divide both sides by c/4 - a, giving
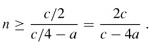
Thus, if we assume that T(n) = O(1) for n < 2c/(c -4a), we have T(n) = O(n). We conclude that any order statistic, and in particular the median, can be determined on average in linear time.