SKEDSOFT

Design Analysis Of Algorithm

Shortest paths and matrix multiplication: This section presents a dynamic-programming algorithm for the all-pairs shortestpaths problem on a directed graph G = (V, E). Each major loop of the dynamic program will invoke an operation that is very similar to matrix multiplication, so that the algorithm will look like repeated matrix multiplication. We shall start by developing a Θ(V4)-time algorithm for the all-pairs shortest-paths problem and then improve its running time to Θ(V3 lg V).

Before proceeding, let us briefly recap the steps given in Dynamic Programming for developing a dynamic-programming algorithm.

  1. Characterize the structure of an optimal solution.

  2. Recursively define the value of an optimal solution.

  3. Compute the value of an optimal solution in a bottom-up fashion.

(The fourth step, constructing an optimal solution from computed information, is dealt with in the exercises.)

The structure of a shortest path: We start by characterizing the structure of an optimal solution. For the all-pairs shortest-paths problem on a graph G = (V, E), we have proven  that all subpaths of a shortest path are shortest paths. Suppose that the graph is represented by an adjacency matrix W = (wij). Consider a shortest path p from vertex i to vertex j, and suppose that p contains at most m edges. Assuming that there are no negative-weight cycles, m is finite. If i = j, then p has weight 0 and no edges. If vertices i and j are distinct, then we decompose path p into 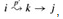, where path p′ now contains at most m - 1 edges.

A recursive solution to the all-pairs shortest-paths problem

Now, let 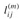be the minimum weight of any path from vertex i to vertex j that contains at most m edges. When m = 0, there is a shortest path from i to j with no edges if and only if i = j. Thus,

For m ≥ 1, we compute 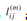as the minimum of 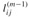(the weight of the shortest path from i to j consisting of at most m - 1 edges) and the minimum weight of any path from i to j consisting of at most m edges, obtained by looking at all possible predecessors k of j. Thus, we recursively define

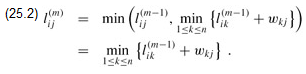
The latter equality follows since wjj = 0 for all j.

What are the actual shortest-path weights δ(i, j)? If the graph contains no negative-weight cycles, then for every pair of vertices i and j for which δ(i, j) < ∞, there is a shortest path from i to j that is simple and thus contains at most n - 1 edges. A path from vertex i to vertex j with more than n - 1 edges cannot have lower weight than a shortest path from i to j. The actual shortest-path weights are therefore given by

Computing the shortest-path weights bottom up

Taking as our input the matrix W = (wij), we now compute a series of matrices L(1), L(2),..., L(n-1), where for m = 1, 2,..., n - 1, we have 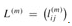. The final matrix L(n-1) contains the actual shortest-path weights. Observe that 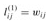for all vertices i, j ∈ V , and so L(1) = W.

The heart of the algorithm is the following procedure, which, given matrices L(m-1) and W, returns the matrix L(m). That is, it extends the shortest paths computed so far by one more edge.

	EXTEND-SHORTEST-PATHS(L, W)
1  n ← rows[L]
2  let 
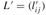
	be an n × n matrix
3  for i ← 1 to n
4      do for j ← to n
5            do 
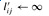
	6              for k ← 1 to n
7                  do 
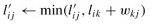
	8  return L′