The Bellman-ford Algorithm

The Bellman-Ford algorithm: The Bellman-Ford algorithm solves the single-source shortest-paths problem in the general case in which edge weights may be negative. Given a weighted, directed graph G = (V, E) with source s and weight function w : E → R, the Bellman-Ford algorithm returns a boolean value indicating whether or not there is a negative-weight cycle that is reachable from the source. If there is such a cycle, the algorithm indicates that no solution exists. If there is no such cycle, the algorithm produces the shortest paths and their weights.

The algorithm uses relaxation, progressively decreasing an estimate d[v] on the weight of a shortest path from the source s to each vertex v ∈ V until it achieves the actual shortest-path weight δ(s, v). The algorithm returns TRUE if and only if the graph contains no negative-weight cycles that are reachable from the source.

	BELLMAN-FORD(G, w, s)
1  INITIALIZE-SINGLE-SOURCE(G, s)
2  for i ← 1 to |V[G]| - 1
3       do for each edge (u, v) ∈ E[G]
4              do RELAX(u, v, w)
5  for each edge (u, v) ∈ E[G]
6       do if d[v] > d[u]   w(u, v)
7             then return FALSE
8  return TRUE

Figure 24.4 shows the execution of the Bellman-Ford algorithm on a graph with 5 vertices. After initializing the d and π values of all vertices in line 1, the algorithm makes |V| - 1 passes over the edges of the graph. Each pass is one iteration of the for loop of lines 2-4 and consists of relaxing each edge of the graph once. Figures 24.4(b)-(e) show the state of the algorithm after each of the four passes over the edges. After making |V|- 1 passes, lines 5-8 check for a negative-weight cycle and return the appropriate boolean value. (We'll see a little later why this check works.)

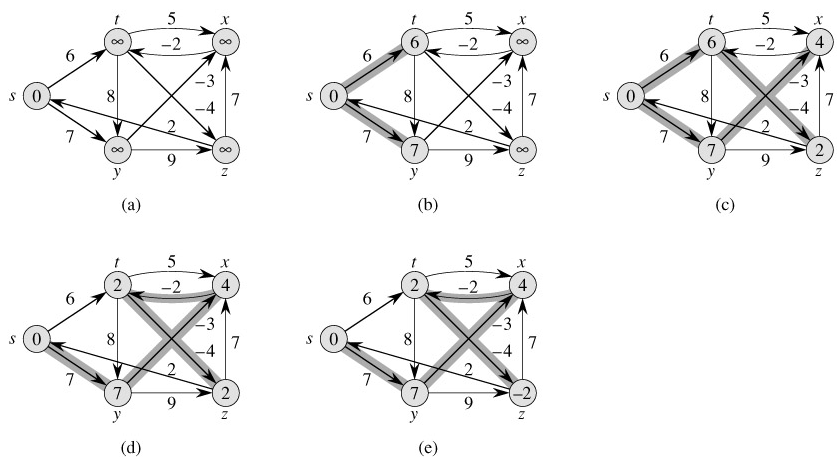
Figure 24.4: The execution of the Bellman-Ford algorithm. The source is vertex s. The d values are shown within the vertices, and shaded edges indicate predecessor values: if edge (u, v) is shaded, then π[v] = u. In this particular example, each pass relaxes the edges in the order (t, x), (t, y), (t, z), (x, t), (y, x), (y, z), (z, x), (z, s), (s, t), (s, y). (a) The situation just before the first pass over the edges. (b)-(e) The situation after each successive pass over the edges. The d and π values in part (e) are the final values. The Bellman-Ford algorithm returns TRUE in this example.

The Bellman-Ford algorithm runs in time O(V E), since the initialization in line 1 takes Θ(V) time, each of the |V| - 1 passes over the edges in lines 2-4 takes Θ(E) time, and the for loop of lines 5-7 takes O(E) time.

To prove the correctness of the Bellman-Ford algorithm, we start by showing that if there are no negative-weight cycles, the algorithm computes correct shortest-path weights for all vertices reachable from the source.

SKEDSOFT