SKEDSOFT
The Floyd-Warshall algorithm: In this section, we shall use a different dynamic-programming formulation to solve the all-pairs shortest-paths problem on a directed graph G = (V, E). The resulting algorithm, known as the Floyd-Warshall algorithm, runs in Θ(V3) time. As before, negative-weight edges may be present, but we assume that there are no negative-weight cycles. As in Shortest paths and matrix multiplication, we shall follow the dynamic-programming process to develop the algorithm. After studying the resulting algorithm, we shall present a similar method for finding the transitive closure of a directed graph.
The structure of a shortest path: In the Floyd-Warshall algorithm, we use a different characterization of the structure of a shortest path than we used in the matrix-multiplication-based all-pairs algorithms. The algorithm considers the "intermediate" vertices of a shortest path, where an intermediate vertex of a simple path p = 〈v1, v2,..., vl〉 is any vertex of p other than v1 or vl, that is, any vertex in the set {v2, v3,..., vl-1}.
The Floyd-Warshall algorithm is based on the following observation. Under our assumption that the vertices of G are V = {1, 2,..., n}, let us consider a subset {1, 2,..., k} of vertices for some k. For any pair of vertices i, j ∈ V, consider all paths from i to j whose intermediate vertices are all drawn from {1, 2,..., k}, and let p be a minimum-weight path from among them. (Path p is simple.) The Floyd-Warshall algorithm exploits a relationship between path p and shortest paths from i to j with all intermediate vertices in the set {1, 2,..., k - 1}. The relationship depends on whether or not k is an intermediate vertex of path p.
-
If k is not an intermediate vertex of path p, then all intermediate vertices of path p are in the set {1, 2,..., k - 1}. Thus, a shortest path from vertex i to vertex j with all intermediate vertices in the set {1, 2,..., k - 1} is also a shortest path from i to j with all intermediate vertices in the set {1, 2,..., k}.
-
If k is an intermediate vertex of path p, then we break p down into
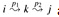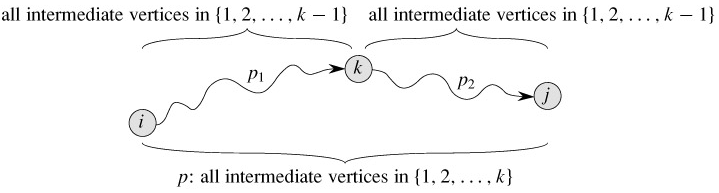
as shown in Figure 25.3. By Lemma 24.1, p1 is a shortest path from i to k with all intermediate vertices in the set {1, 2,..., k}. Because vertex k is not an intermediate vertex of path p1, we see that p1 is a shortest path from i to k with all intermediate vertices in the set {1, 2,..., k - 1}. Similarly, p2 is a shortest path from vertex k to vertex j with all intermediate vertices in the set {1, 2,..., k - 1}.
-
Figure 25.3: Path p is a shortest path from vertex i to vertex j, and k is the highest-numbered intermediate vertex of p. Path p1, the portion of path p from vertex i to vertex k, has all intermediate vertices in the set {1, 2,..., k - 1}. The same holds for path p2 from vertex k to vertex j.
A recursive solution to the all-pairs shortest-paths problem
Based on the above observations, we define a recursive formulation of shortest-path estimates that is different from the one in Shortest paths and matrix multiplication. Let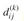 
be the weight of a shortest path from vertex i to vertex j for which all intermediate vertices are in the set {1, 2,..., k}. When k = 0, a path from vertex i to vertex j with no intermediate vertex numbered higher than 0 has no intermediate vertices at all. Such a path has at most one edge, and hence 
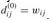. A recursive definition following the above discussion is given by
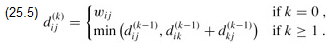
Because for any path, all intermediate vertices are in the set {1, 2,..., n}, the matrix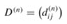 
gives the final answer: 
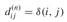for all i, j ∈ V.
Computing the shortest-path weights bottom up
Based on recurrence (25.5), the following bottom-up procedure can be used to compute the values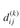 
in order of increasing values of k. Its input is an n × n matrix W defined as in equation (25.1). The procedure returns the matrix D(n) of shortest-path weights.
FLOYD-WARSHALL(W) 1 n ← rows[W] 2 D(0) ← W 3 for k ← 1 to n 4 do for i ← 1 to n 5 do for j ← 1 to n 6 do
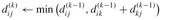
7 return D(n)
Figure 25.4 shows the matrices D(k) computed by the Floyd-Warshall algorithm for the graph in Figure 25.1.
