SKEDSOFT

Suppose that the ith operation on the stack is MULTIPOP(S, k) and that ′ = min(k, s) objects are popped off the stack. The actual cost of the operation is ′, and the potential difference is

Φ(D_i) - Φ(D_i-1) - -′.

Thus, the amortized cost of the MULTIPOP operation is

Similarly, the amortized cost of an ordinary POP operation is 0.

The amortized cost of each of the three operations is O(1), and thus the total amortized cost of a sequence of n operations is O(n). Since we have already argued that Φ(D_i) ≥ Φ(D₀), the total amortized cost of n operations is an upper bound on the total actual cost. The worst-case cost of n operations is therefore O(n).

Incrementing a binary counter: As another example of the potential method, we again look at incrementing a binary counter. This time, we define the potential of the counter after the ith INCREMENT operation to be b_i , the number of ′s in the counter after the ith operation.

Let us compute the amortized cost of an INCREMENT operation. Suppose that the ith INCREMENT operation resets t_i bits. The actual cost of the operation is therefore at most t_i 1, since in addition to resetting t_i bits, it sets at most one bit to 1. If b_i = 0, then the ith operation resets all k bits, and so b_i-1 = t_i = k. If b_i > 0, then b_i = b_i-1 - t_i 1. In either case, b_i ≤ b_i-1 - t_i 1, and the potential difference is

The amortized cost is therefore

If the counter starts at zero, then Φ(D₀) = 0. Since Φ(D_i) ≥ 0 for all i, the total amortized cost of a sequence of n INCREMENT operations is an upper bound on the total actual cost, and so the worst-case cost of n INCREMENT operations is O(n).

The potential method gives us an easy way to analyze the counter even when it does not start at zero. There are initially b₀ ′s, and after n INCREMENT operations there are b_n 1's, where 0 ≤ b₀, b_n ≤ k. (Recall that k is the number of bits in the counter.) We can rewrite equation (17.3) as

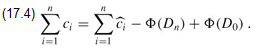
We have ≤ 2 for all 1 ≤ i ≤ n. Since Φ(D₀) = b₀ and Φ(D_n) = b_n, the total actual cost of n INCREMENT operations is

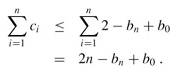
Note in particular that since b₀ ≤ k, as long as k = O(n), the total actual cost is O(n). In other words, if we execute at least n = Ω(k) INCREMENT operations, the total actual cost is O(n), no matter what initial value the counter contains.