SKEDSOFT
The relabel-to-front algorithm: The push-relabel method allows us to apply the basic operations in any order at all. By choosing the order carefully and managing the network data structure efficiently,. We shall now examine the relabel-to-front algorithm, a push-relabel algorithm whose running time is O(V3), which is asymptotically at least as good as O(V2E), and better for dense networks.
The relabel-to-front algorithm maintains a list of the vertices in the network. Beginning at the front, the algorithm scans the list, repeatedly selecting an over-flowing vertex u and then "discharging" it, that is, performing push and relabel operations until u no longer has a positive excess. Whenever a vertex is relabeled, it is moved to the front of the list (hence the name "relabel-to-front") and the algorithm begins its scan anew.
The correctness and analysis of the relabel-to-front algorithm depend on the notion of "admissible" edges: those edges in the residual network through which flow can be pushed. After proving some properties about the network of admissible edges, we shall investigate the discharge operation and then present and analyze the relabel-to-front algorithm itself.
Admissible edges and networks: If G = (V, E) is a flow network with source s and sink t, f is a preflow in G, and h is a height function, then we say that (u, v) is an admissible edge if cf(u, v) > 0 and h(u) = h(v) 1. Otherwise, (u, v) is inadmissible. The admissible network is Gf,h = (V, Ef,h), where Ef,h is the set of admissible edges.
The admissible network consists of those edges through which flow can be pushed. The following lemma shows that this network is a directed acyclic graph (dag).
Neighbor lists: Edges in the relabel-to-front algorithm are organized into "neighbor lists." Given a flow network G = (V, E), the neighbor list N[u] for a vertex u ∈ V is a singly linked list of the neighbors of u in G. Thus, vertex v appears in the list N[u] if (u, v) ∈ E or (v, u) ∈ E. The neighbor list N[u] contains exactly those vertices v for which there may be a residual edge (u, v). The first vertex in N[u] is pointed to by head[N[u]]. The vertex following v in a neighbor list is pointed to by next-neighbor[v]; this pointer is NIL if v is the last vertex in the neighbor list.
The relabel-to-front algorithm cycles through each neighbor list in an arbitrary order that is fixed throughout the execution of the algorithm. For each vertex u, the field current[u] points to the vertex currently under consideration in N[u]. Initially, current[u] is set to head[N[u]].
Discharging an overflowing vertex: An overflowing vertex u is discharged by pushing all of its excess flow through admissible edges to neighboring vertices, relabeling u as necessary to cause edges leaving u to become admissible. The pseudocode goes as follows.
DISCHARGE(u) 1 while e[u] > 0 2 do v ← current[u] 3 if v = NIL 4 then RELABEL(u) 5 current[u] ← head[N[u]] 6 elseif cf(u, v) > 0 and h[u] = h[v] 1 7 then PUSH(u, v) 8 else current[u] ← next-neighbor[v]
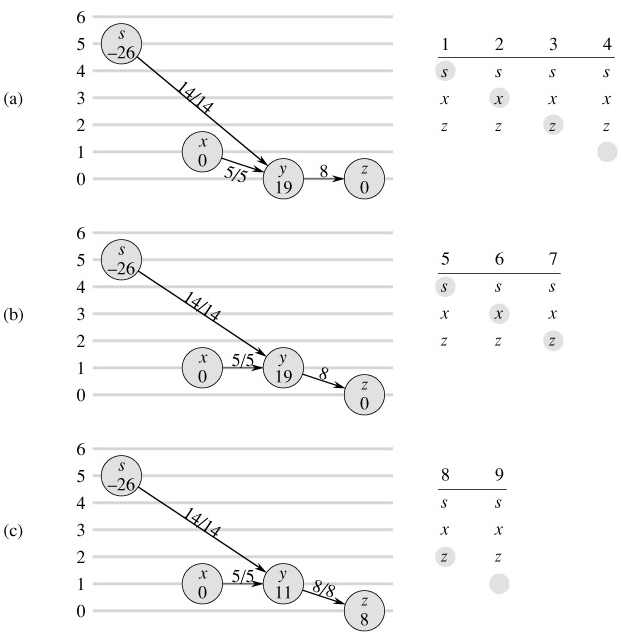
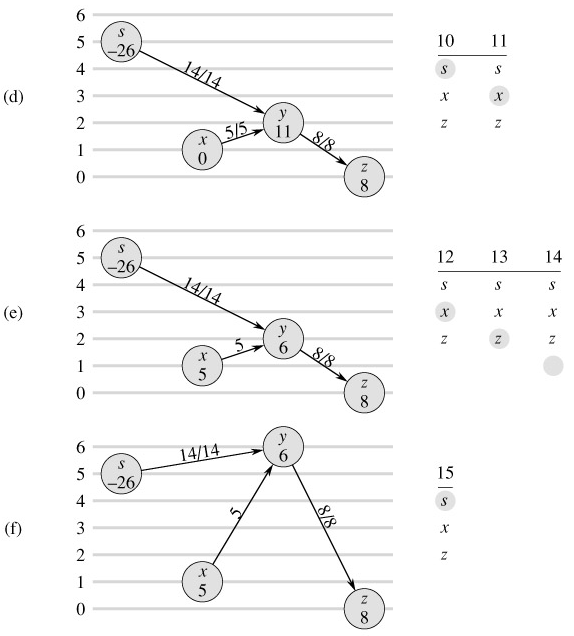
Figure 26.9 steps through several iterations of the while loop of lines 1-8, which executes as long as vertex u has positive excess. Each iteration performs exactly one of three actions, depending on the current vertex v in the neighbor list N[u].
-
If v is NIL, then we have run off the end of N[u]. Line 4 relabels vertex u, and then line 5 resets the current neighbor of u to be the first one in N[u]. (Lemma 26.30 below states that the relabel operation applies in this situation.)
-
If v is non-NIL and (u, v) is an admissible edge (determined by the test in line 6), then line 7 pushes some (or possibly all) of u's excess to vertex v.
-
If v is non-NIL but (u, v) is inadmissible, then line 8 advances current[u] one position further in the neighbor list N[u].