SKEDSOFT
then we can trim L to obtain
L′ = 〈10, 12, 15, 20, 23, 29〉,
where the deleted value 11 is represented by 10, the deleted values 21 and 22 are represented by 20, and the deleted value 24 is represented by 23. Because every element of the trimmed version of the list is also an element of the original version of the list, trimming can dramatically decrease the number of elements kept while keeping a close (and slightly smaller) representative value in the list for each deleted element. The following procedure trims list L = 〈y1, y2, ..., ym〉 in time Θ(m), given L and δ, and assuming that L is sorted into monotonically increasing order. The output of the procedure is a trimmed, sorted list.
TRIM(L, δ) 1 m ← |L| 2 L′ ← 〈y1〉 3 last ← y1 4 for i ← 2 to m 5 do if yi > last · (1 δ) ▹ yi ≥ last because L is sorted 6 then append yi onto the end of L′ 7 last ← yi 8 return L′
The elements of L are scanned in monotonically increasing order, and a number is put into the returned list L′ only if it is the first element of L or if it cannot be represented by the most recent number placed into L′. Given the procedure TRIM, we can construct our approximation scheme as follows. This procedure takes as input a set S = {x1, x2, ..., xn} of n integers (in arbitrary order), a target integer t, and an "approximation parameter" ∈, where
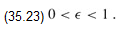
It returns a value z whose value is within a 1 ∈ factor of the optimal solution.
APPROX-SUBSET-SUM(S, t, ∈) 1 n ← |S| 2 L0 ← 〈0〉 3 for i ← 1 to n 4 do Li ← MERGE-LISTS(Li-1, Li-1 xi) 5 Li ← TRIM(Li, ∈/2n) 6 remove from Li every element that is greater than t 7 let z* be the largest value in Ln 8 return z*
Line 2 initializes the list L0 to be the list containing just the element 0. The for loop in lines 3-6 has the effect of computing Li as a sorted list containing a suitably trimmed version of the set Pi , with all elements larger than t removed. Since Li is created from Li-1, we must ensure that the repeated trimming doesn't introduce too much inaccuracy. In a moment, we shall see that APPROX-SUBSET-SUM returns a correct approximation if one exists. As an example, suppose we have the instance
S = 〈104, 102, 201, 101〉
with t = 308 and ∈ = 0.40. The trimming parameter δ is ∈/8 = 0.05. APPROX-SUBSET-SUM computes the following values on the indicated lines:
| line 2: | L0 | = | 〈0〉, |
| line 4: | L1 | = | 〈0, 104〉, |
| line 5: | L1 | = | 〈0, 104〉, |
| line 6: | L1 | = | 〈0, 104〉, |
| line 4: | L2 | = | 〈0, 102, 104, 206〉, |
| line 5: | L2 | = | 〈0, 102, 206〉, |
| line 6: | L2 | = | 〈0, 102, 206〉, |
| line 4: | L3 | = | 〈0, 102, 201, 206, 303, 407〉 |
| line 5: | < L3 | = | 〈0, 102, 201, 303, 407〉 |
| line 6: | L3 | = | 〈0, 102, 201, 303〉 |
| line 4: | L4 | = | 〈0, 101, 102, 201, 203, 302, 303, 404〉 |
| line 5: | L4 | = | 〈0, 101, 201, 302, 404〉 |
| line 6: | L4 | = | 〈0, 101, 201, 302〉 |
The algorithm returns z* = 302 as its answer, which is well within ∈ = 40% of the optimal answer 307 = 104 102 101; in fact, it is within 2%.