SKEDSOFT

The following theorem shows that this problem is NP-complete.

Theorem: The vertex-cover problem is NP-complete.

Proof We first show that VERTEX-COVER ∈ NP. Suppose we are given a graph G = (V, E) and an integer k. The certificate we choose is the vertex cover V' ⊆ V itself. The verification algorithm affirms that |V'| = k, and then it checks, for each edge (u, v) ∈ E, that u ∈ V' or v ∈ V'. This verification can be performed straightforwardly in polynomial time.

We prove that the vertex-cover problem is NP-hard by showing that CLIQUE ≤_P VERTEX-COVER. This reduction is based on the notion of the "complement" of a graph. Given an undirected graph G = (V, E), we define the complement of G as 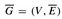, where 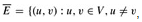, and (u, v) ∉ E}. In other words, 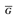is the graph containing exactly those edges that are not in G. Figure 34.15 shows a graph and its complement and illustrates the reduction from CLIQUE to VERTEX-COVER.

The reduction algorithm takes as input an instance 〈G, k〉 of the clique problem. It computes the complement 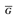, which is easily done in polynomial time. The output of the reduction algorithm is the instance 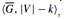, of the vertex-cover problem. To complete the proof, we show that this transformation is indeed a reduction: the graph G has a clique of size k if and only if the graph 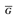has a vertex cover of size |V | - k.

Suppose that G has a clique V' ⊆ V with |V'| = k. We claim that V - V' is a vertex cover in 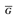. Let (u, v) be any edge in Ē. Then, (u, v) ∉ E, which implies that at least one of u or v does not belong to V', since every pair of vertices in V' is connected by an edge of E. Equivalently, at least one of u or v is in V - V', which means that edge (u, v) is covered by V - V'. Since (u, v) was chosen arbitrarily from Ē, every edge of Ē is covered by a vertex in V - V'. Hence, the set V - V', which has size |V | - k, forms a vertex cover for .

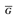Conversely, suppose that 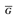has a vertex cover V' ⊆ V, where |V'| = |V| - k. Then, for all u, v ∈ V, if (u, v) ∈ Ē, then u ∈ V' or v ∈ V' or both. The contrapositive of this implication is that for all u, v ∈ V, if u ∉ V' and v ∉ V', then (u, v) E. In other words, V -V' is a clique, and it has size |V |-|V'| = k.

Since VERTEX-COVER is NP-complete, we don't expect to find a polynomial-time algorithm for finding a minimum-size vertex cover. The vertex-cover problempresents a polynomial-time "approximation algorithm," however, which produces "approximate" solutions for the vertex-cover problem. The size of a vertex cover produced by the algorithm is at most twice the minimum size of a vertex cover.

Thus, we shouldn't give up hope just because a problem is NP-complete. There may be a polynomial-time approximation algorithm that obtains near-optimal solutions, even though finding an optimal solution is NP-complete. Approximation Algorithms gives several approximation algorithms for NP-complete problems.