SKEDSOFT

Topological sort: This section shows how depth-first search can be used to perform a topological sort of a directed acyclic graph, or a "dag" as it is sometimes called. A topological sort of a dag G = (V, E) is a linear ordering of all its vertices such that if G contains an edge (u, v), then u appears before v in the ordering. (If the graph is not acyclic, then no linear ordering is possible.) A topological sort of a graph can be viewed as an ordering of its vertices along a horizontal line so that all directed edges go from left to right. Topological sorting is thus different from the usual kind of "sorting" studied in Sorting and Order Statistics.

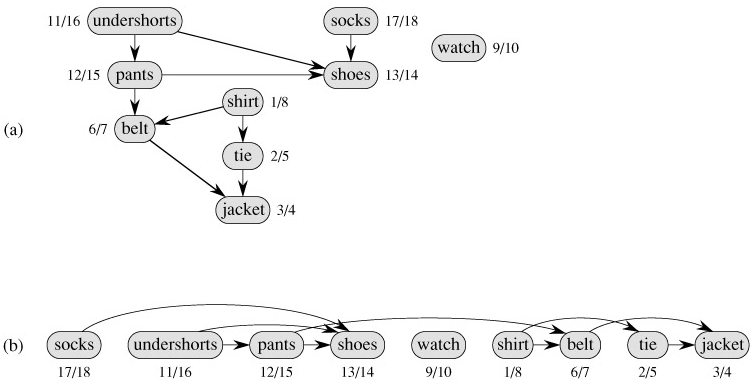
Directed acyclic graphs are used in many applications to indicate precedences among events. Figure 22.7 gives an example that arises when Professor Bumstead gets dressed in the morning. The professor must don certain garments before others (e.g., socks before shoes). Other items may be put on in any order (e.g., socks and pants). A directed edge (u, v) in the dag of Figure 22.7(a) indicates that garment u must be donned before garment v. A topological sort of this dag therefore gives an order for getting dressed. Figure 22.7(b) shows the topologically sorted dag as an ordering of vertices along a horizontal line such that all directed edges go from left to right.

The following simple algorithm topologically sorts a dag.

	TOPOLOGICAL-SORT(G)
1  call DFS(G) to compute finishing times f[v] for each vertex v
2  as each vertex is finished, insert it onto the front of a linked list
3  return the linked list of vertices

Figure 22.7(b) shows how the topologically sorted vertices appear in reverse order of their finishing times.

We can perform a topological sort in time Θ(V E), since depth-first search takes Θ(V E) time and it takes O(1) time to insert each of the |V| vertices onto the front of the linked list.

We prove the correctness of this algorithm using the following key lemma characterizing directed acyclic graphs.

Lemma 22.11