SKEDSOFT

Adjacency Matrices: Carrying out graph algorithms using the representation of graphs by lists of edges, or by adjacency lists, can be cumbersome if there are many edges in the graph. To simplify computation, graphs can be represented using matrices. Two types of matrices commonly used to represent graphs will be presented here. One is based on the adjacency of vertices, and the other is based on incidence of vertices and edges.

Suppose that G = (V ,E) is a simple graph where |V| = n. Suppose that the vertices of G are listed arbitrarily as v1, v2, . . . , vn. The adjacency matrix A (or AG) of G, with respect to this listing of the vertices, is the n x n zero–one matrix with 1 as its (i, j )th entry when vi and vj are adjacent, and 0 as its (i, j )th entry when they are not adjacent. In other words, if its adjacency matrix is A = [aij ], then

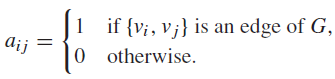
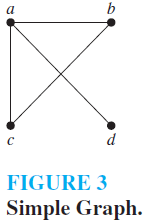
EXAMPLE 1 Use an adjacency matrix to represent the graph shown in Figure 3.
Solution:We order the vertices as a, b, c, d. The matrix representing this graph is

EXAMPLE 1 Draw a graph with the adjacency matrix

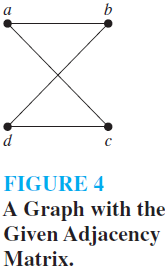
            with respect to the ordering of vertices a, b, c, d.

Solution: A graph with this adjacency matrix is shown in Figure 4.
Note that an adjacency matrix of a graph is based on the ordering chosen for the vertices. Hence, there may be as many as n! different adjacency matrices for a graph with n vertices, because there are n! different orderings of n vertices.

The adjacency matrix of a simple graph is symmetric, that is, aij = aji , because both of these entries are 1 when vi and vj are adjacent, and both are 0 otherwise. Furthermore, because a simple graph has no loops, each entry aii, i = 1, 2, 3, . . . , n, is 0.

Adjacency matrices can also be used to represent undirected graphs with loops and with multiple edges. A loop at the vertex vi is represented by a 1 at the (i, i)th position of the adjacency matrix. When multiple edges connecting the same pair of vertices vi and vj, or multiple loops at the same vertex, are present, the adjacency matrix is no longer a zero–one matrix, because the (i, j )th entry of this matrix equals the number of edges that are associated to {vi , vj }. All undirected graphs, including multigraphs and pseudographs, have symmetric adjacency matrices.

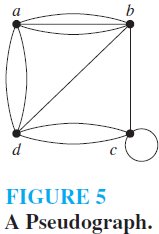
EXAMPLE 2 Use an adjacency matrix to represent the pseudograph shown in Figure 5.

We used zero–one matrices in Chapter 9 to represent directed graphs. The matrix for a directed graph G = (V ,E) has a 1 in its (i, j )th position if there is an edge from vi to vj , where v1, v2, . . . , vn is an arbitrary listing of the vertices of the directed graph. In other words, if A = [aij ] is the adjacency matrix for the directed graph with respect to this listing of the vertices, then

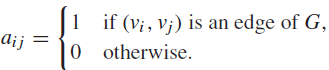
The adjacency matrix for a directed graph does not have to be symmetric, because there may not be an edge from vj to vi when there is an edge from vi to vj .

Adjacency matrices can also be used to represent directed multigraphs. Again, such matrices are not zero–one matrices when there are multiple edges in the same direction connecting two vertices. In the adjacency matrix for a directed multigraph, aij equals the number of edges that are associated to (vi , vj ).