SKEDSOFT

Predicates : A predicate is a statement containing one or more variables.
Proposition : If values are assigned to all the variables in a predicate, the resulting statement is a proposition.
e.g. 1. x < 9 is a predicate
2. 4 < 9 is a proposition

Propositional Function : Let a be a given set. A propositional function (or : on open sentence or condition) defined on A is an expression P(x) which has the
property that P(a) is true or false for each a ∈ A.
The set A is called domain of P(x) and the set Tp of all elements of A for which P (a) is true is called the truth set of P(x).
i.e.   Another use of predicates is in programming Two common constructions are “if P(x), then execute certain steps” and “while Q(x), do specified actions.” The predicates P(x) and Q(x) are called the guards for the block of programming code often the guard for a block is a conjunction or disjunction.

e.g. Let A = {x / x is an integer < 8}
Here P(x) is the sentence “x is an integer less than 8”.
The common property is “an integer less than 8”.
P(1) is the statement “1 is an integer less than 8”.
P(1) is true, 1 ∈ A etc

Quantifiers : The expressions ‘ for all’ and ‘there exists’ are called quantifiers. The process of applying quantifier to a variable is called quantification of variables.

Universal quantification : The universal quantification of a predicate P(x) is the statement, “For all values of x, P(x) is true.” The universal quantification of P(x) is denoted by v for all x P(x). The symbol is called the universal quantifier.
e.g. 1) The sentence P(x) : - (-x) = x is a predicate that makes sense for real numbers x. The universal quantification of P(x), x P(x) is a true statement because for all real numbers, -(- x) = x.
2) Let Q(x) : x 1 < 5, then Q(x) : x < 5 is a false statement, as Q(5) is not true. Universal quantification can also be stated in English as “for every x”, “every x”, or “for any x.”

Existential quantification - The existential quantification of a predicate P(x) is the statement “There exists a value of x for which P(x) is true.”
The existential quantification of P(x) is denoted ∃xP(x) . The symbol ∃ is called the existential quantifier.
e.g. 1) Let Q : x 1< 4 . The existential quantification of Q(x), ∃xQ(x) is a true statement, because Q(2) is true statement.
2) The statement ∃y, y 2 = y is false. There is no value of y for which the propositional function y 2=y produces a true statement.

Negation of Quantified statement :

This is true for any proposition p(x). DeMorgan’s Law.

The result for universal and existential quantifiers is as follows.

1)  

In other words, the following two statements are equivalent.
i) It is not true that, for all a ∈ A, P(a) is true.

ii) There exists an a ∈ A, such that P(a) is false.
II)
That is, the following two statements are equivalent.
i) It is not true that for some a ∈ A, P(a) is true.
ii) For all a ∈ A, P(a) is false.
Other several properties for the universal and existential quantifiers are………

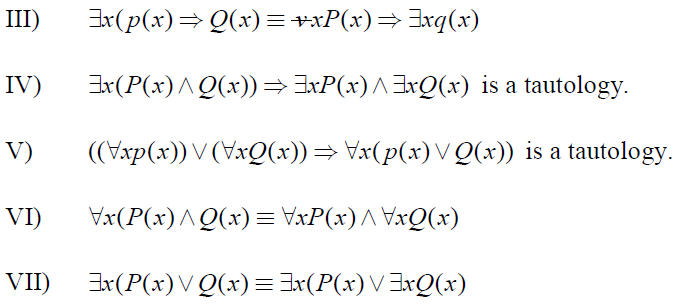
Example  : Express the statement using quantifiers. “Every student in your school has a computer or has a friend who has a computer.”

Solution :
Let c(x) : “x has a computer”
F(x,y) : “x and y are friends”
We have