SKEDSOFT

Introduction: We have discussed rules of inference for propositions.We will nowdescribe some important rules of inference for statements involving quantifiers. These rules of inference are used extensively in mathematical arguments, often without being explicitly mentioned.

Universal instantiation is the rule of inference used to conclude that P(c) is true, where c is a particular member of the domain, given the premise ∀xP(x). Universal instantiation is used when we conclude from the statement “All women are wise” that “Lisa is wise,” where Lisa is a member of the domain of all women.

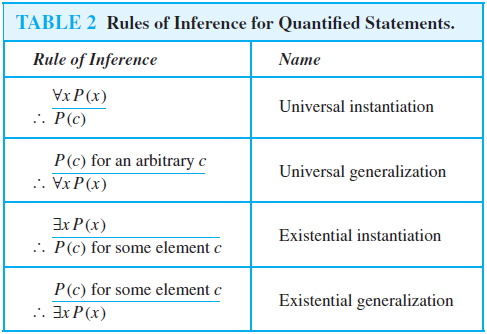
Universal generalization is the rule of inference that states that ∀xP(x) is true, given the premise that P(c) is true for all elements c in the domain. Universal generalization is used when we show that ∀xP(x) is true by taking an arbitrary element c from the domain and showing that P(c) is true. The element c that we select must be an arbitrary, and not a specific, element of the domain. That is, when we assert from ∀xP(x) the existence of an element c in the domain, we have no control over c and cannot make any other assumptions about c other than it comes from the domain. Universal generalization is used implicitly in many proofs in mathematics and is seldom mentioned explicitly. However, the error of adding unwarranted assumptions about the arbitrary element c when universal generalization is used is all too common in incorrect reasoning.

Existential instantiation is the rule that allows us to conclude that there is an element c in the domain for which P(c) is true if we know that ∃xP(x) is true.We cannot select an arbitrary value of c here, but rather it must be a c for which P(c) is true. Usually we have no knowledge of what c is, only that it exists. Because it exists, we may give it a name (c) and continue our argument.

Existential generalization is the rule of inference that is used to conclude that ∃xP(x) is true when a particular element c with P(c) true is known. That is, if we know one element c in the domain for which P(c) is true, then we know that ∃xP(x) is true. We summarize these rules of inference in Table 2.We will illustrate how some of these rules of inference for quantified statements are used in Examples 1 and 2.

EXAMPLE 1 Show that the premises “Everyone in this discrete mathematics class has taken a course in computer science” and “Marla is a student in this class” imply the conclusion “Marla has taken a course in computer science.”
Solution: Let D(x) denote “x is in this discrete mathematics class,” and let C(x) denote “x has taken a course in computer science.” Then the premises are ∀x(D(x) → C(x)) and D(Marla). The conclusion is C(Marla).
The following steps can be used to establish the conclusion from the premises.

EXAMPLE 2 Show that the premises “A student in this class has not read the book,” and “Everyone in this class passed the first exam” imply the conclusion “Someone who passed the first exam has not read the book.”
Solution: Let C(x) be “x is in this class,” B(x) be “x has read the book,” and P(x) be “x passed the first exam.” The premises are ∃x(C(x)∧¬B(x)) and ∀x(C(x) → P(x)). The conclusion is ∃x(P(x)∧¬B(x)). These steps can be used to establish the conclusion from the premises.