SKEDSOFT

Introduction: A set is to be thought of as any collection of objects whatsoever. The objects can also be anything and they are called elements of the set. The elements contained in a given set need not have anything in common (other than the obvious common attribute that they all belong to the given set). Equally, there is no restriction on the number of elements allowed in a set; there may be an infinite number, a finite number or even no elements at all. There is, however, one restriction we insist upon: given a set and an object, we should be able to decide (in principle at least—it may be difficult in practice) whether or not the object belongs to the set. Clearly a concept as general as this has many familiar examples as well as many frivolous ones.

Notation: We shall generally use upper-case letters to denote sets and lower-case letters to denote elements. (This convention will sometimes be violated, for example when the elements of a particular set are themselves sets.) The symbol ∈ denotes ‘belongs to’ or ‘is an element of’. Thus a ∈ A means (the element) a belongs to (the set) A and a / ∈ A means ¬(a ∈ A) or a does not belong to A.

Defining Sets: Sets can be defined in various ways. The simplest is by listing the elements enclosed between curly brackets or ‘braces’ { }. The two (well defined) sets in examples 3.1 could be written:
A = {Picasso, Eiffel Tower, π}
B = {2, 4, 6, 8, . . .}.

In the second of these we clearly cannot list all the elements. Instead we list enough elements to establish a pattern and use ‘. . . ’ to indicate that the list
continues indefinitely. Other examples are the following.

For a fixed positive integer n, Cn = {1, 2, . . . , n}, the set of the first n positive integers. Againwe use ‘. . . ’ to indicate that there are elements in the list which we have omitted to write, although in this case only finitely many are missing.

D = { }, the empty set (or null set), which contains no elements. This set is usually denoted φ. Listing the elements of a set is impractical except for small sets or sets where there is a pattern to the elements such as B and Cn above. An alternative is to define the elements of a set by a property or predicate (see chapter 1). More precisely, if P(x) is a single-variable propositional function, we can form the set whose elements are all those objects a (and only those) for which P(a) is a true proposition. A set defined in this way is denoted
A = {x : P(x)}.
(This is read: the set of all x such that P(x) (is true).)

Note that ‘within A’—that is, if we temporarily regard A as the universe of discourse—the quantified propositional function ∀x P(x) is a true statement.

Equality of Sets: Two sets are defined to be equal if and only if they contain the same elements; that is, A = B if ∀x[x ∈ A ↔ x ∈ B] is a true proposition, and conversely. The order in which elements are listed is immaterial. Also, it is the standard convention to disregard repeats of elements in a listing. Thus the following all define the same set:

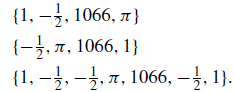
We should perhaps note here that there is only one empty set; or, put another way, all empty sets are equal. This is because any two empty sets contain precisely the same elements: none!
Also, if P(x) and Q(x) are propositional functions which are true for precisely the same objects x, then the sets they define are equal, i.e.

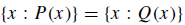
For example, {x : (x − 1)² = 4} = {x : (x 1)(x − 3) = 0}, since the two propositional functions P(x) : (x − 1)² = 4 and Q(x) : (x 1)(x − 3) = 0 are true for precisely the same values of x, namely −1 and 3.

Other notations commonly used for the cardinality of A are n(A), #(A) and ¯¯A

Although cardinality appears to be a simple enough concept, determining the cardinality of a given set may be difficult in practice. This is particularly the case when some or all of the elements of the given set are themselves sets. This is a perfectly valid construction: the elements of a set can be anything, so certainly they can be sets.

For example, let X = {{1, 2}}. Then X contains only a single element, namely the set {1, 2}, so |X| = 1. It is clearly important to distinguish between the set {1, 2} (which has cardinality 2) and X, the set which has {1, 2} as its only element. Similarly, the sets φ and {φ} are different. The latter is non-empty since it contains a single element—namely φ. Thus |{φ}| = 1.