SKEDSOFT

DIRAC’S THEOREM: Let G be a graph of order p ≥ 3. If deg v ≥ p/2 for every vertex v of G, then G is hamiltonian.
Proof. If p = 3, then the condition on G implies that G ≅ k3 and hence G is hamiltonian. We may assume, therefore, that p ≥ 4.
Let P : v1, v2, ....... vn be a longest path in G (see Figure). Then every neighbour of v1 and every neighbour of vn is on P.

Otherwise, there would be a longer path than P.
Consequently, n ≥ 1 p/2 .
There must be some vertex vi where 2 ≤ i ≤ n, such that v1 is adjacent to vi and vn is adjacent to vi – 1.
If this were not the case, then whenever v1 is adjacent to a vertex vi, the vertex vn is not adjacent to vi – 1.
Since atleast p/2  of p – 1 vertices different from vn are not adjacent to vn.
Hence, deg vn ≤ (P – 1) – p/2  < p/2 , which contradicts the fact that deg vn ≥ p/2 .

Therefore as we claimed, there must be a vertex vi adjacent to v1 and vi – 1 is adjacent to vn (see Figure).

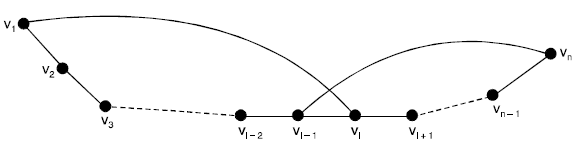
We now see that G has cycle C : v1, vi, vi 1, ...... vn – 1, vn, vi – 1, vi – 2, ......, v2, v1 that contains all the vertices of P. If C contains all the vertices of G (if n = p) then C is a hamiltonian cycle, and the proof. Otherwise, there is some vertex u of G that is not on C.
By hypothesis, deg u ≥ p/2. Since P contains at least 1 p/2 vertices, there are fewer than p/2 vertices not on C ; so u must be adjacent to a vertex v that lies on C.
However, the edge uv plus the cycle C contain a path whose length is greater than that of P, which is impossible. Thus C contains all vertices of G and G is hamiltonian. Hence the proof.

Let G be a graph with p-vertices. If deg v ≥ (p-1)/2 for every vertex v of G then G contains a hamiltonian path.
Proof. If p = 1 then G ≅ k1 and G contains a (trivial) Hamiltonian path. Suppose then that p ≥ 2 and define H = G k1.
Let v denote the vertex of H that is not in C. Since H has vertex p 1, it follows that deg v ≥ p. Moreover, for every vertex u of G,

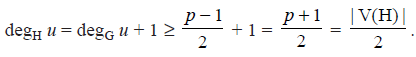
By Dirac’s theorem, H contains a hamiltonian cycle C. By removing the vertex v from C, we obtain a hamiltonian path in G.

Hence the proof.

Theorem Let G be a simple graph with n vertices and let u and v be an edge. Then G is hamiltonian if and only if G uv is hamiltonian.
Proof. Suppose G is hamiltonian. Then the super graph G uv must also be hamiltonian. Conversely, suppose taht G uv is hamiltonian. Then if G is not hamiltonian. i.e., if G is a graph with p ≥ 3 vertices such that for all non adjacent vertices u and v, deg u deg v ≥ p.
We obtain the inequality deg u deg v < n.
However by hypothesis, deg u deg v ≥ n.
Hence G must be hamiltonian. This completes the proof.