SKEDSOFT

We observe that K4* has four vertices and six edges. Also, every two vertices of K4* are joined by an edge. This means that K4* also represents the complete graph of four vertices. As such, K4 and K4* are isomorphic. In other words, K4 is a self-dual graph.

Dual of a subgraph: Let G be a planar graph and G* be its geometric dual. Let e be an edge in G and e* be its dual in G*. Consider the subgraph G – e got by deleting e from G. Then, the geometric dual of G – e can be constructed as explained in the two possible cases.

Case (1) : Suppose e is on a boundary common to two regions in G. Then the removal of e from G will merge these two regions into one. Then the two corresponding vertices in G* get merged into one, and the edge e* gets deleted from G*.
Thus, in this case, the dual of G – e can be obtained from G* by deleting the edge e* and then fusing the two end vertices of e* in G* – e*.

Case (2) : Suppose e is not on a boundary common to two regions in G. Then e is a pendant edge and e* is a self-loop. The dual of G – e is now the same as G* – e*. Thus, the geometric dual of G – e can be constructed for all choices of the edge e of G. Since every subgraph H of a graph is of the form G – s where s is a set edges of G.

Dual of a homeomorphic graph: Let G be a planar graph and G* be its geometric dual.
Let e be an edge in G and e* be its dual in G*.
Suppose we create an additional vertex in G by introducing a vertex of degree 2 in the edge e.
This will simply add an edge parallel to e* in G*. If we merge two edges in series in G then one of the corresponding parallel edges in G* will be eliminated. The dual of any graph homeomorphic to G can be obtained from G*.

Abstract dual: Given two graphs G1 and G2, we say that G1 and G2 are abstract duals of each other if there is a one-to-one correspondence between the edges in G1 and the edges in G2, with the property that a set of edges in G1 forms a circuit in G1 if and only if the corresponding set of edges in G2 forms a cut-set in G2. Consider the graphs G1 and G2 shown in Figure (2.62).

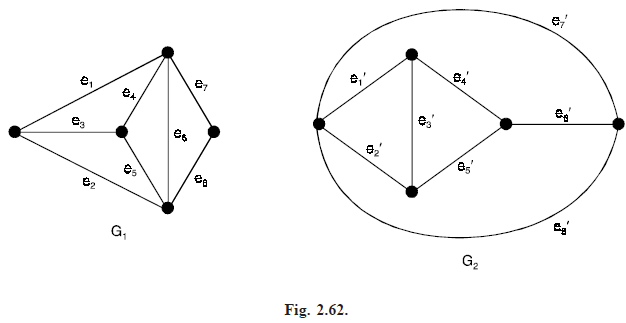
We observe that there is a one-to-one correspondence between the edges in G1 and the edges in G2 with the edge ei in G1 corresponding to the edge ei′ in G2, i = 1, 2, ...... 8.

Further, note that a set of edges in G1 which forms a circuit in G1 corresponds to a set of edges in G2 which forms a cut sets in G2.
For example, {e6, e7, e8} is a circuit in G1 and {e6′, e7′, e8′) is a cut-set in G2. Accordingly, G1 and G2 are abstract duals of each other.

Combinatorial dual: Given two planar graphs G1 and G2, we say that they are combinatorial duals of each other if there is a one-to-one correspondence between the edges of G1 and G2 such that if H1 is any subgraph of G1 and H2 is the corresponding subgraph of G2, then

Rank of (G2 – H2) = Rank of G2 – Nullity of H1

Consider the graph G1 and G2 shown in Figure (2.62) above, and their subgraphs H1 and H2 shown in Figure (2.64)(a, b).

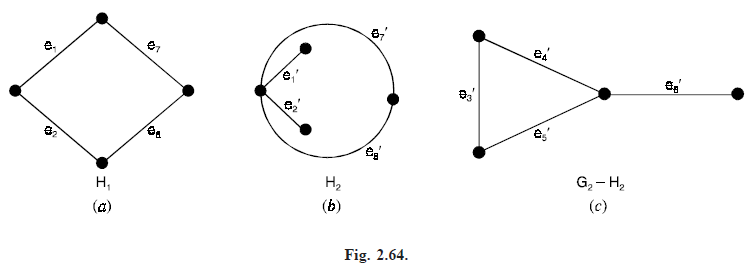
Note that there is one-to-one correspondence between the edges of G1 and G2 and that the subgraphs H1 and H2 correspond to each other. The graph of G2 – H2 is shown in Figure (2.64)(c). This graph is disconnected and has two components.

Rank of G2 = 5 – 1 = 4, Rank of H1 = 4 – 1 = 3  Nullity of H1 = 4 – 3 = 1
Rank of (G2 – H2) = 5 – 2 = 3.
⇒ Rank of (G2 – H2) = 3 = Rank of G2 – Nullity of H1.
Hence, G1 and G2 are combinatorial duals of each other.