SKEDSOFT

Frequency assignments: Television channels 2 through 13 are assigned to stations in New Delhi so that no two stations within 150 miles can operate on the same channel. How can the assignment of channels be modeled by graph colouring ?

Solution. Construct a graph by assigning a vertex to each station.
Two vertices are connected by an edge if they are located within 150 miles of each other.
An assignment of channels corresponds to a colouring of the graph. Where each colour represents a different channel.

Index registers: In efficient compilers the execution of loops is speeded up when frequently used variables are stored temporarily in index registers in the central processing unit, instead of in regular memory. For a given loop, how many index registers are needed ?
Solution. This problem can be addressed using a graph colouring model. To set up the model, let each vertex of a graph represent a variable in the loop. There is an edge between two vertices if the variables they represent must be stored in index registers at the same time during the execution of the loop. Thus, the chromatic number of the graph gives the number of index registers needed, since different registers must be assigned to variables when the vertices respresenting these variables are adjacent in the graph.

Problem. What is the chromatic number of the graph Cn ?
Solution. We will first consider some individual cases.
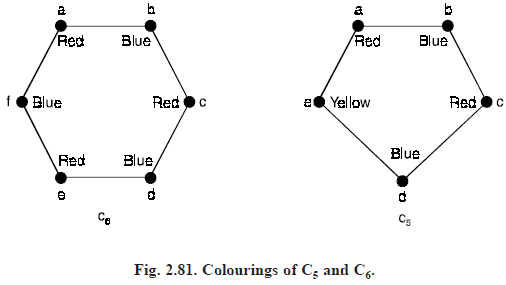
To begin, let n = 6. Pick a vertex and colour it red.
Proceed clockwise in the planar depiction of C6 shown in Figure (2.81).
It is necessary to assign a second colour, say blue, to the next vertex reached.
Continue in the clockwise direction, the third vertex can be coloured red, the fourth vertex blue, and the fifth vertex red.
Finally, the sixth vertex, which is adjacent to the first, can be coloured blue.
Hence, the chromatic number of C6 is 2. Figure (2.81) displays the colouring constructed here.
Next, let n = 5 and consider C5. Pick a vertex and colour it red.
Proceeding clockwise, it is necessary to assign a second colour, say blue, to the next vertex reached.
Continuing in the clockwise direction, the third vertex can be coloured red, and the fourth vertex can be coloured blue.
The fifth vertex cannot be coloured either red or blue, since it is adjacent to the fourth vertex and the first vertex.
Consequently, a third colour is required for this vertex.
Note that we would have also needed three colours if we had coloured vertices in the counter clockwise direction.
Thus, the chromatic number of C5 is 3. A colouring of C5 using three colours is displayed in Figure (2.81).

In general, two colours are needed to colours Cn when n is even. To construct such a colouring, simply pick a vertex and colour it red.
Proceeding around the graph in a clockwise direction (using a planar representation of the graph) colouring the second vertex blue, the third vertex red, and so on.
The nth vertex can be colored blue, since the two vertices adjacent to it, namely the (n – 1)st and the first vertices, are both coloured red.
When n is odd and n > 1, the chromatic number of Cn is 3.
To see this, pick an initial vertex. To use only two colours, it is necessary to alternate colours as the graph is traversed in a clockwise direction.
However, the nth vertex reached is adjacent to two vertices of different colours, namely, the first and (n – 1)st. Hence, a third colour must be used.