SKEDSOFT

OPERATIONS OF GRAPHS

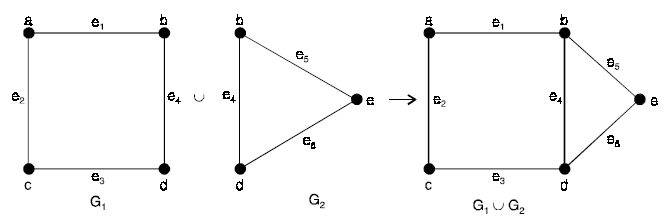
Union: Given two graphs G1 and G2, their union will be a graph such that
V(G1 ∪ G2) = V(G1) ∪ V(G2)
and E(G1 ∪ G2) = E(G1) ∪ E(G2)

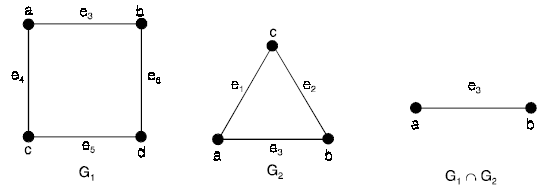
Intersection: Given two graphs G1 and G2 with at least one vertex in common then their intersection will be a graph such that
V(G1 ∩ G2) = V(G1) ∩ V(G2)
and E(G1 ∩ G2) = E(G1) ∩ E(G2)

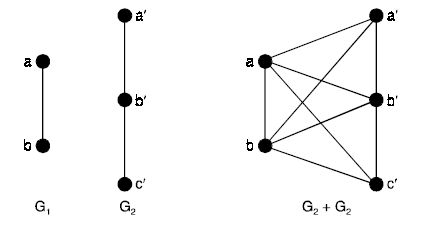
Sum of two graphs: If the graphs G1 and G2 such that V(G1) ∩ V(G2) = φ, then the sum G1 G2 is defined as the graph whose vertex set is V(G1) V(G2) and the edge set is consisting those edges, which are in G1 and in G2 and the edges obtained, by joining each vertex of G1 to each vertex of G2.
For example,

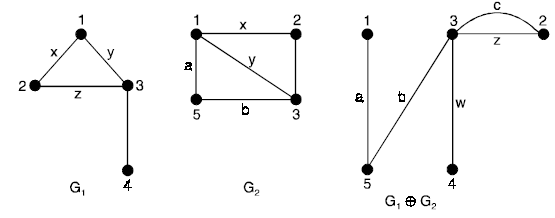
Ring sum: Let G1 (V1, E1) and G2 (V2, E2) be two graphs. Then the ring sum of G1 and G2, denoted by G1 ⊕ G2 is defined as the graph G such that :
(i) V(G) = V(G1) ∪ V(G2)
(ii) E(G) = E(G1) ∪ E(G2) – E(G1) ∩ E(G2)
i.e., the edges that either in G1 or G2 but not in both. The ring sum of two graphs G1 and G2 is shown below.

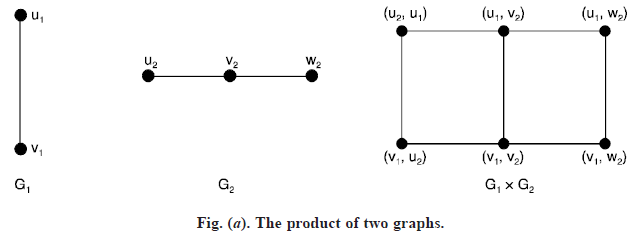
Product of graphs: To define the product G1 × G2 of two graphs consider any two points u = (u1, u2) and v = (v1, v2) in V = V1 × V2. Then u and v are adjacent in G1 × G2 whenever [u1 = v1 and u2 adj. v2] or [u2 = v1 and u1 adj. v1]
For example,