SKEDSOFT

Reachability: A node v in a simple graph G is said to be reachable from the vertex u of G if there exists a from u to v the set of vertices which a path from u to v, the set of vertices which are reachable from a given vertex v is called the reachable set of v and is denoted by R(v). For any subset U of the vertex set V, the reachable set of U is the set of all vertices which are reachable from any vertex set of S and this set is denoted by R(S).
For example, in the graph given below :

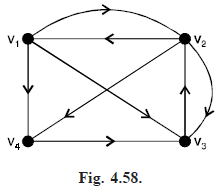
R(v1) = {v2, v3, v4}, R(v2) = {v1, v3, v4} and R({v1, v2}) = {v3, v4}.

Distance and diameter: In a connected graph G, the distance between the vertices u and v, denoted by d(u, v) is the length of the shortest path.
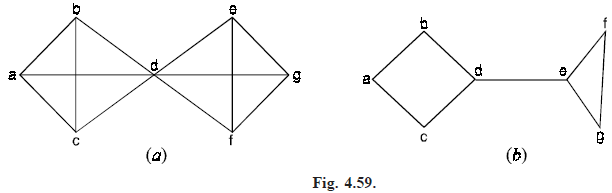
In Fig. (4.59)(a), d(a, f) = 2 and in Fig. (4.59) (b), d(a, e) = 3.

The distance function as defined above has the following properties. If u, v and w are any three verties of a connected graph then
(i) d(u, v) ≥ 0 and d(u, v) = 0 if u = v.
(ii) d(u, v) = d(v, u) and
(iii) d(u, v) ≥ d(u, w) d(w, v)
This shows that distance in a graph is metric. The diameter of G, written as diam (G) is the maximum distance between any two vertices in G. In Fig. (4.59) (a), diam (G) = 2 and in Fig. (4.59) (b), diam (G) = 4.

Cut vertex, cut set and bridge: Sometimes the removal of a vertex and all edges incident with it produces a subgraph with more connected components. A cut vertex of a connected graph G is a vertex whose removal increases the number of components. Clearly if v is a cut vertex of a connected graph G, G – v is disconnected.
A cut vertex is also called a cut point.
Analogously, an edge whose removal produces a graph with more connected components then the original graph is called a cut edge or bridge.
The set of all minimum number of edges of G whose removal disconnects a graph G is called a cut set of G. Thus a cut set S of a satisfy the following :
(i) S is a subset of the edge set E of G.
(ii) Removal of edges from a connected graph G disconnects G.
(iii) No proper subset of G satisfy the condition.

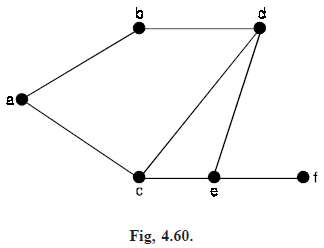
In the graph in Figure below, each of the sets {{b, d}, {c, d}, {c, e}} and {{e, f}} is a cut set. The edge {e, f} is the only bridge. The singleton set consisting of a bridge is always a cut of set of G.
Connected or weakly connected: A directed graph is called connected at weakly connected if it is connected as an undirected graph in which each directed edge is converted to an undirected graph.
Unilaterally connected: A simple directed graph is said to be unilaterally connected if for any pair of vertices of the graph atleast one of the vertices of the pair is reachable from other vertex.

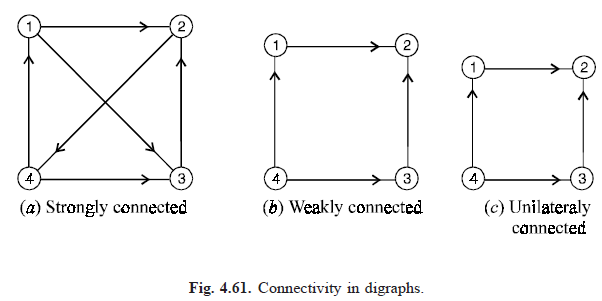
Strongly connected: A directed graph is called strongly connected if for any pair of vertices of the graph both the vertices of the pair are reachable from one another. For the diagraphs is Fig. (4.61) the digraph in (a) is strongly connected, in a (b) it is weakly connected, while in (c) it is unilaterally connected but not strongly connected.

Note that a unilaterally connected digraph is weakly connected but a weakly connected digraph
is not necessarily unilateraly connected. A strongly connected digraph is both unilaterally and weakly
connected.
Connectivity: To study the measure of connectedness of a graph G we consider the minimum number of vertices and edges to be removed from the graph in order to disconnect it.
Edge connectivity: Let G be a connected graph. The edge connectivity of G is the minimum number of edges whose removal results in a disconnected or trivial graph. The edge connectivity of a connected graph G is denoted by λ(G) or E(G).

(i) If G is a disconnected graph, then λ(G) or E(G) = 0.
(ii) Edge connectivity of a connected graph G with a bridge is 1.

Vertex connectivity: Let G be a connected graph. The vertex connectivity of G is the minimum number of vertices whose removal results in a disconnected or a trivial graph. The vertex connectivity of a connected graph is denoted by k(G) or V(G)
(i) If G is a disconnected graph, then λ(G) or E(G) = 0.
(ii) Edge connectivity of a connected graph G with a bridge is 1.
(iii) The complete graph kn cannot be disconnected by removing any number of vertices, but the removal of n – 1 vertices results in a trivial graph. Hence k(kn) = n – 1.
(iv) The vertex connectivity of a graph of order atleast there is one if and only if it has a cut vertex.
(v) Vertex connectivity of a path is one and that of cycle Cn (n ≥ 4) is two.