SKEDSOFT

Transport Network: Let N = (V, E) be a loop-free connected directed graph. Then N is called a network, or transport network, if the following conditions are satisfied :
(i) There exists a unique vertex a ∈ V with id(a), the in degree of a, equal to O. This vertex a is called the source.
(ii) There is a unique vertex z ∈ V, called the sink, where od(z), the out degree of z, equals O.
(iii) The graph N is weighted, so there is a function from E to the set of non negative integers that assigns to each edge e = (v, w) ∈ E a capacity, denoted by c(e) = c(v, w).
If N = (V, E) is a transport network, a function f from E to the non negative integers is called a flow for N if

(i) f(e) ≤ c(e) for each edge e ∈ E, and
(ii) for each v ∈ V, other than the source a or the sink z,
If there is no edge (v, w), then f(v, w) = 0.
Let f be a flow for a transport network N = (V, E)
(i) An edge e of the network is called saturated if f(e) = c(e). When f(e) < c(e), the edge is
called unsaturated.
(ii) If a is the source of N, then val(f) = 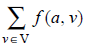is called the value of the flow.
If N = (V, E) is a transport network and C is a cut-set for the undirected graph associated with N, then C is called a cut, or an a–z cut, if the removal of the edges in C from the network results in the separation of a and z.

For example, the graph in Fig. (4.67) is a transport network. Here vertex a is the source, the sink is at vertex z, and capacities are shown beside each edge. Since c(a, b) c(a, g) = 5 7 = 12, the amount of the commodity being transported from a to z cannot exceed 12. With c(d, z) c(h, z) = 5 6 = 11, the amount is further restricted to be no greater than 11.

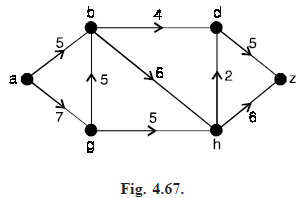
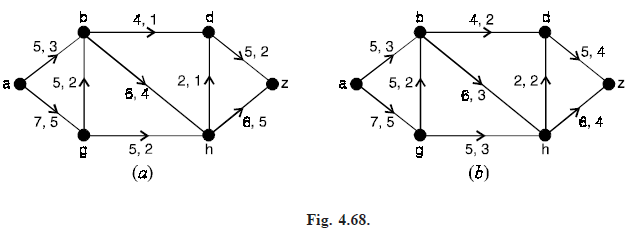
For the network in Fig. (4.68), the label x, y on each edge e is determined so that x = c(e) and y is the value assigned for a possible flow f. The label on each edge e satisfies f(e) ≤ c(e).
In part (a) of the Fig. (4.68), the flow into vertex g is 5, but the flow out from that vertex is 2 2 = 4.
Hence the function f is not a flow in this case.

For the network in Fig. (4.68) (b), only the edge (h, d) is saturated. All other edges are unsaturated. The value of the flow in this network is

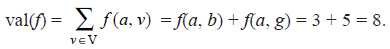
We observe that in the network of Fig. (4.68) (b)

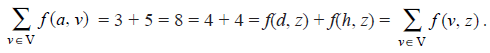
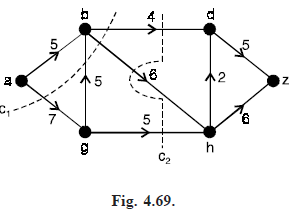
Consequently, the total flow leaving the source a equals the total flow into the sink z. Fig. (4.69) indicates a cut for the given network (dotted curves). The cut C, consists of the undirected edges {a, g}, {b, d}, {b, g} and {b, h}. This cut partitions the vertices of the network into the two sets P = {a, b} and its complement P = {d, g, h, z}, so C1 is denoted as (P, P ).

The capacity of a cut, denoted C(P, P ), is defined by C(P, P ) = the sum of the capacities of all edges (v, w), where v ∈ P and w ∈ P .
In this example, C(P, P ) = c(a, g) c(b, d) c(b, h) = 7 4 6 = 17.
The cut c2 induces the vertex partition Q = {a, b, g}. Q = {d, h, z} and has capacity c(Q, Q) = c(b, d) c(b, h) c(g, h) = 4 6 5 = 15.