SKEDSOFT

Partial Derivatives:

Given a function of one variable say f(x); we define the derivative of f(x) at x = a to be

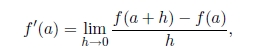
provided this limit exists. For a function of several variables the totalderivative of a function is not as easy to define, however, if we set all but one of the independent variables equal to a constant, we can define the partial derivative of a function by using a limit similar to the one above. For example, if f is a function of the variables x; y and z, we can set x = a and y = b and define the partial derivative of f with respect to z to be

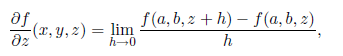
wherever this limit exists. Note that the partial derivative is a function of all three variables x; y and z: The partial derivative of f with respect to z gives the instantaneous rate of change of f in the z direction. The definition for the partial derivative of f with respect to x or y is defined in a similar way. Computing partial derivatives is no harder than computing ordinary one-variable derivatives; one simply treats the fixed variables as constants.

Examples-1: Suppose

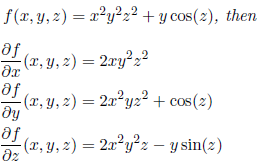
We can take heigher order partial derivatives by continuing in the same manner. In the example above first taking the partial derivatives of f with respect to y and then with respect to z yield.

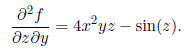
Such aderivatives is called mixed partial derivatives of f. From a well known theorem of advanced calculus, if the second order partial derivatives of f exists in a neighborhood of the point (a,b,c) are continuous at (a,b,c) then the mixed partial derivatives do not depend on the order in which they are derived.

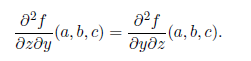
This result was first proved by Leonard Euler.