SKEDSOFT
Taylor’s Theorem:
Taylor's Theorem for a function of a single variable and Maclaurin's series functions. Suppose a function f (x) satiesfy the following conditions:
1. f (x), f' (x), f'' (x),........ f (n-1) (x) are continuous in the closed intervals [a,b]
2. f (n-1) (x) is differentiable i.e fn (x) exists in the open intervals (a,b)
Then there exists a point c ∈ (a,b) such that;
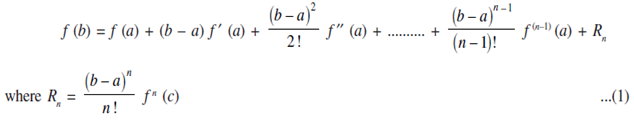
Taylor's Theorem is more usually written in the following forms. Substitute b = x in the above equations we get;
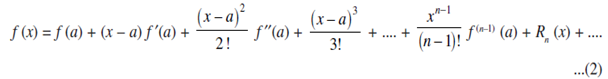
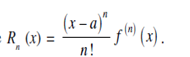
Thus f (x) can be expressed as the sum of infinite series. This series is called the Taylor's series for the function f (x) about the point a. If we substitute a = 0 we get;
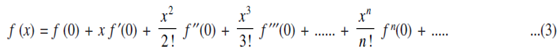
This is called Macluarin's series for the function f (x). If f (x) = y and f' (x), f'' (x), .................. are denoted by y1, y2, ................... The Macluarin's series can also be written in the form:
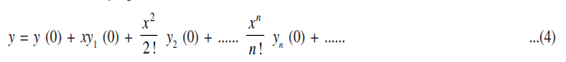
Rolle’s Theorem:
If a function f (x) is:
1. Continuous in a closed interval [a, b],
2. Differentiable in the open interval (a, b) and
3. f (a) = f (b). Then there exists at least one value c of x in (a, b) such that f ′ (c) = 0