SKEDSOFT
Concept of Moment:
In statistics moment are defined as the mean values of powers of the deviation in any individual series or frequency distribution (discrete and continuous) taken about three points:
(i) Origin
(ii) Mean
(iii) Any other point.
Moments about Origin:
For an Individual Series In case of individual series x1,x2, . . . ,xn, rth moment about origin is denoted by μ′r and is defined as
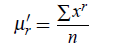
where r = 1,2,3,4,...
For an Frequency Distribution If x1,x2, ...,xn are the values of a variable x with the corresponding frequencies f1, f2, ..., fn respectively, then rth moment about origin is denoted by μ′r and is defined as
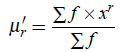
For an Frequency Distribution For grouped data, let x1,x2, ...,xn be taken as the mid-values then we have
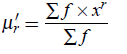
where r = 1,2,3,4, ....
Moments about Mean:
For an Individual Series In case of individual series x1,x2, . . . ,xn, rth moment about mean is denoted by μ′r and is defined as
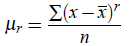
where r = 1,2,3,4, ....
For an Frequency Distribution If x1,x2, ...,xn are the values of a variable x with the corresponding frequencies f1, f2, ..., fn respectively, then rth moment about mean is denoted by μ′r and is defined as
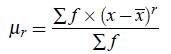
where r = 1,2,3,4, ....
For an Frequency Distribution For grouped data, let x1,x2, ...,xn be taken as the mid-values then we have
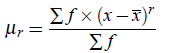
where r = 1,2,3,4, ....