SKEDSOFT
Kurtosis:
Definition 7. Kurtosis refers to the extent to which unimodal frequency curve is peaked.
Definition 8. Kurtosis is a measure that refers to the peakedness of the top of the curve . Kurtosis gives the degree of flatness or peakedness in the region about the mode of a frequency distribution.
According to Croxton and Cowden,
Definition 9. A measure of kurtosis indicates the degree to which the curve of a frequency distribution is peaked or flat topped.
According to Clark and Sckkade,
Definition 10. Kurtosis is the property of a frequency distribution which expresses its relative peakedness.
Karl Pearson in 1905 introduced the three types of curves on the basis of kurtosis:
Mesokurtic: If the concentration of frequency in the middle of the frequency distribution is normal, the curve is known as mesokurtic.
Leptokurtic: If the frequencies are densely concentrated in the middle of the series, the will be more peaked than normal and is known as Leptokurtic.
Platykurtic: If the frequencies are not densely concentrated in the middle of the series, the curve will be more flat than normal and is known as platykurtic.
Measure of Kurtosis:
The measure of kurtosis based on central moments are given by Karl Pearson:
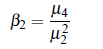
- if β2 = 3, the curve is Mesokurtic or normal
- if β2 > 3, the curve is Leptokurtic or more peaked
- if β2 < 3, the curve is Platykurtic or flat topped.
The measure of Kurtosis is also represented by gamma two, 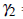 = β2−3
= β2−3
-
if
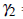 = 0,the curve is Mesokurtic
= 0,the curve is Mesokurtic -
if
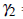 > 0,the curve in Leptokurtic
> 0,the curve in Leptokurtic -
if
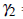 < 0, the curve is Platykurtic.
< 0, the curve is Platykurtic.
Probability Mass Function (PMF):
If X is a discrete random variable with distinct values x1, x2, . . . ,xn for which X has positive probabilities p1, p2, . . . , pn, then the function f (x) defined as:
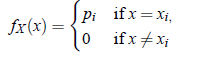
is called the probability mass function of random variable X. Since P(S) = 1(Probability of sure event is one.), we must have
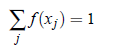
Probability Density Function (PDF):
Similar to PMF, probability density function is defined for continuous random variable X. The funxtion f (x) defined as
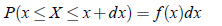
such that,