SKEDSOFT

Random Variable:

In an experiment of tossing a pair of coin we may be interested in obtaining the probabilities of getting 0,1 or 2 heads which are possible events. We consider a variable X which hold these possible values 0,1 or 2. This variable is a real valued function defined over sample space whose range is non empty set of real numbers is called random variable. i.e, A random variable is a function X(w) with domain S and range (−infinite,infinite) such that for every real number a, the event [e : X(e) ≤ a].

Mathematical Expectation or Expected Value of a Random Variable:

The expected value of a discrete random variable is a weighted average of all possible values of the random variable, where the weights are the probabilities associated with the corresponding values. For discret random variable. The expected value of a discrete random variable X with probability mass function (p.m.f) f (x) is given below:

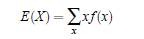
For continuous random variable. The mathematical expression for computing the expected value of a continuous random varriable X with probability density function (p.d.f.) f(x) is, however, as follows:

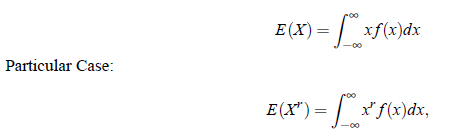
which is defined as μ′_r the rth moment (about origin) of the probability distribution. Thus

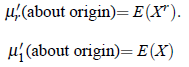
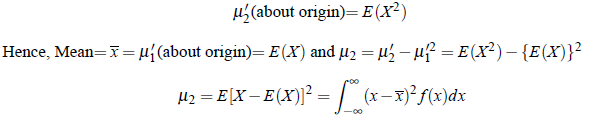
Properties of Expectation:

1. Addition theorem: If X and Y are random variables, then E(aX bY) = aE (X) bE (Y) and we can generalise above result as 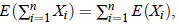if all the expectations exist.

2. Multiplication theorem: If X andY are random variables, then E(XY) = E(X) E(Y) provided X and Y are independent and we can generalise above result as 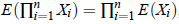if all the expectations exist.

3. Expectation of a linear Combination of Random Variable: Let X₁,X₂, . . . ,Xn be any n random variables and if a₁,a₂, . . . ,a_n are any n constants, then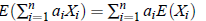

4. If X ≥ 0 then E (X) ≥ 0.

5. If X, Y are two random variable s.t.Y ≤ X, then E(Y) ≤ E(X)

6. | E(X)| ≤ E(|X|)