SKEDSOFT
 Denavit-Hartenberg Notation
Denavit-Hartenberg Notation
To formulate robot kinematics, we wish to present a homogeneous transformation matrix representing a general coordinate transformation from one link of a robot to an adjacent link.
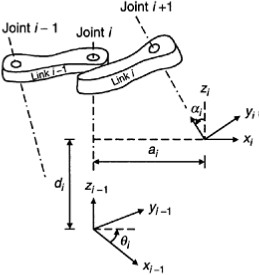
For this purpose, body frames, fixed to links of the robot, are chosen according to the Denavit-Hartenberg notation. This is explained in Figure.
Note that joint i joins link i-1 with link i. Frame i, which is the body frame of link i, has its z axis located at joint i 1. If the joint is revolute, then the joint rotation is about the z axis. If the joint is prismatic, the joint translation is along the z axis.
It is seen from Figure that frame i can be obtained by transforming frame i-1 as follows:
1. Rotate frame i-1 through qi about the z axis.
2. Translate the new frame through di along the z axis.
3. Translate the new frame through ai along the new x axis.
4. Rotate the new frame through ai about the current x axis.
Note that all these movements are carried out in the positive sense of a right-handed Cartesian frame.
The homogeneous transformation matrix Ai which represents the overall link-to-link transformation is obtained by the product of the four 4×4 transformation matrices corresponding to the above four steps, when taken in the proper order (i.e., 1×2×3×4).
It can be easily verified that this matrix is given by:
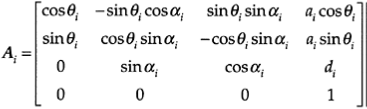
For a revolute joint, the joint coordinate would be:
Qi=qi
and, for a prismatic joint, the joint coordinate would be:
Qi=ai
with the remaining parameters in Ai kept constant. Hence, the only variable in Aiis qi.
The base frame, frame 0, is assumed fixed. This is taken as the inertial frame with respect to which a robotic task is specified.
For an n degree-of-freedom robot, the body frame of the end effector is frame n, and this frame moves with the end effector.
It follows that the position and orientation of the end effector frame, expressed in the base frame, is given by the columns of the overall homogeneous transformation matrixT
T=A1(q1)A2(q2) ···An(qn)