SKEDSOFT

Natural Frequency Equivalence

Now consider the approach of natural frequency equivalence. Here we derive an equivalent lumped-parameter model by equating the fundamental (lowest) natural frequency of the distributed-parameter system to the natural frequency of the lumped-parameter model (in the one-degree-of-freedom case).

The method can be easily extended to multidegree-of-freedom lumped parameter models as well. We will illustrate our approach by using an example.

A heavy spring of mass ms and stiffness ks with one end fixed and the other end attached to a sliding mass m, is shown in Figure (a).

If the mass m is sufficiently larger than ms, then at relatively high frequencies the mass will virtually stand still. Under these conditions we have the configuration shown in Figure (b), where the two ends of the spring are fixed.

Also, approximate the distributed mass by an equivalent mass me at the mid

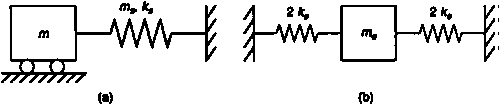
Point of the spring: each spring segment has double the stiffness of the original spring. Hence the overall stiffness is 4ks. The natural frequency of the lumped-model is

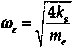
It is known from a complete analysis of a heavy spring that the natural frequency for the fixed-fixed configuration is

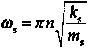
Where n is the mode number. Then, for the fundamental (first) mode (i.e., n=1), the natural frequency equivalence gives

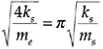
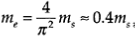
Note that since the effect of inertia decreases with frequency, it is not necessary to consider the case of low frequencies.

The natural frequency equivalence may be generalized as eigenvalueequivalence (pole equivalence) for any dynamic system.

 In this case, the eigenvalues of the lumped parameter model are equated to the corresponding eigenvalues of the distributed-parameter system, and the model parameters are determined accordingly.