SKEDSOFT
Error of interpolation: No numerical result has meaning without an estimate of the error. The exponential integral function we are attempting to interpolate is not a polynomial, so a polynomial representation is bound to be inexact.
We assume that f(x) has continuous derivatives of order up to n 1 for all x ∈ (a, b). Since, f(x) is approximated by Pn(x), the results contain errors. We define the error of interpolation or truncation error as
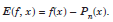....................1.1
Without giving the derivation, we write the expression for the error of interpolation as
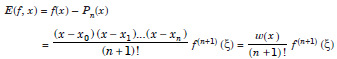....................1.2
where min(x0, x1,..., xn, x) < ξ < max(x0, x1,..., xn, x).
Since, ξ is an unknown, it is difficult to find the value of the error. However, we can find a bound of the error. The bound of the error is obtained as
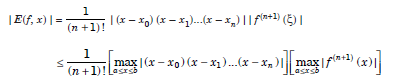....................1.3
Note that in (1.1), we compute the maximum absolute value of w(x) = (x – x0)(x – x1)...(x – xn), that is max | w(x) | and not the maximum of w(x).
Since the interpolating polynomial is unique, the error of interpolation is also unique, that is, the error is same whichever form of the polynomial is used.
Example: Using the data sin(0.1) = 0.09983 and sin (0.2) = 0.19867, find an approximatevalue of sin (0.15) by Lagrange interpolation. Obtain a bound on the error at x = 0.15.
Solution: We have two data values. The Lagrange linear polynomial is given by
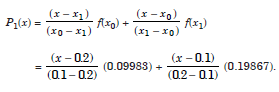
Hence,
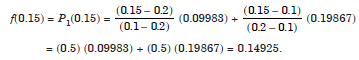
The truncation error is given by
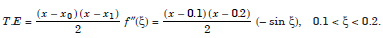
since f(x) = sin x. At x = 0.15, we obtain the bound as
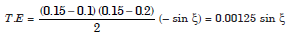
and
