SKEDSOFT
There are two methods through which we can solve the roots the polynomial equations.
- Direct Method.
- Iterative methods.
Direct methods These methods give the exact values of all the roots in a finite number of steps (disregarding the round-off errors). Therefore, for any direct method, we can give the total number of operations (additions, subtractions, divisions and multiplications). This number is called the operational count of the method.
For example, the roots of the quadratic equation ax2 bx c = 0, a ≠ 0, can be obtained using the method
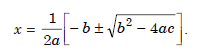
For this method, we can give the count of the total number of operations.
There are direct methods for finding all the roots of cubic and fourth degree polynomials.However, these methods are difficult to use.
Direct methods for finding the roots of polynomial equations of degree greater than 4 or transcendental equations are not available in literature.
Iterative methods These methods are based on the idea of successive approximations. We start with one or two initial approximations to the root and obtain a sequence of approximations
x0, x1, ..., xk, ..., which in the limit as k → ∞, converge to the exact root α.
An iterative method for finding a root of the equation f(x) = 0 can be obtained as
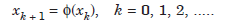
This method uses one initial approximation to the root x0. The sequence of approximations is given by
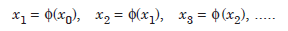
The function φ is called an iteration function and x0 is called an initial approximation.
If a method uses two initial approximations x0, x1, to the root, then we can write the method as
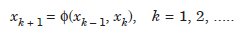
Convergence of iterative methods The sequence of iterates, {xk}, is said to converge to the exact root α, if
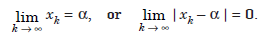
The error of approximation at the kth iterate is defined as εk = xk – α. Then, we can write the above equation,
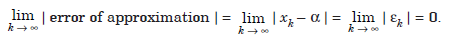
Criterion to terminate iteration procedure Since, we cannot perform infinite number of iterations, we need a criterion to stop the iterations. We use one or both of the following criterion.
(i) The equation f(x) = 0 is satisfied to a given accuracy or f(xk) is bounded by an error tolerance ε.
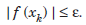
(ii) The magnitude of the difference between two successive iterates is smaller than a given accuracy or an error bound ε.
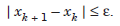
Generally, we use the second criterion. In some very special problems, we require to use both the criteria.
For example, if we require two decimal place accuracy, then we iterate until | xk 1 – xk | < 0.005. If we require three decimal place accuracy, then we iterate until| xk 1– xk | < 0.0005.