SKEDSOFT
To see that propagation is really a wave disturbance, take y-component of Eqn. (3) and x-component of Eqn. (4)
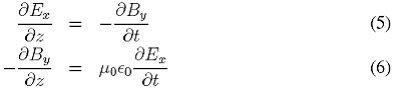
To get the wave equation for  , take the derivative of eqn. (5) with respect to
, take the derivative of eqn. (5) with respect to  and substitute in eqn. (6) and interchange the space and time derivatives,
and substitute in eqn. (6) and interchange the space and time derivatives,








Similarly, we can show, We get
Each of the above equations represents a wave disturbance propagating in the z-direction with a speed

On substituting numerical values, the speed of electromagnetic waves in vacuum is  m/sec.
m/sec.
Consider plane harmonic waves of angular frequency  and wavlength
and wavlength  . We can express the waves as
. We can express the waves as

The amplitudes  an
an  are not independent as they must satisfy eqns. (5) and (6) :
are not independent as they must satisfy eqns. (5) and (6) :

Using Eqn. (5) we get
The ratio of the electric field amplitude to the magnetic field amplitude is given by
Fields  and
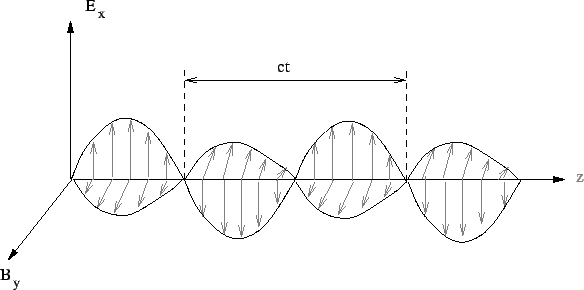
and  are in phase, reaching their maximum and minimum values at the same time. The electric field oscillates in the x-z plane and the magnetic field oscillates in the y-z plane. This corresponds to a polarized wave . Conventionally, the plane in which the electric field oscillates is defined as the plane of polarization. In this case it is x-z plane. The figure shows a harmonic plane wave propagating in the z-direction. Note that
are in phase, reaching their maximum and minimum values at the same time. The electric field oscillates in the x-z plane and the magnetic field oscillates in the y-z plane. This corresponds to a polarized wave . Conventionally, the plane in which the electric field oscillates is defined as the plane of polarization. In this case it is x-z plane. The figure shows a harmonic plane wave propagating in the z-direction. Note that  and the direction of propagation
and the direction of propagation  form a right handed triad.
form a right handed triad.
