SKEDSOFT
Magnetism in Matter: we have seen that in the presence of an electric field, a dielectric gets polarized, leading to bound charges. The polarization vector is, in general, in the direction of the applied electric field.
A similar phenomenon occurs when a material medium is subjected to an external magnetic field. However, unlike the behaviour of dielectrics in electric field, different types of material behave in different ways when an external magnetic field is applied.
We have seen that the source of magnetic field is electric current. The circulating electrons in an atom, being tiny current loops, constitute a magnetic dipole with a magnetic moment whose direction depends on the direction in which the electron is moving. An atom as a whole, may or may not have a net magnetic moment depending on the way the moments due to different elecronic orbits add up. (The situation gets further complicated because of electron spin, which is a purely quantum concept, that provides an intrinsic magnetic moment to an electron.)
In the absence of a magnetic field, the atomic moments in a material are randomly oriented and consequently the net magnetic moment of the material is zero. However, in the presence of a magnetic field, the substance may acquire a net magnetic moment either in the direction of the applied field or in a direction opposite to it. The former class of material is known as paramagnetic material while the latter is called diamagnetic.
When a paramagenetic material is subjected to a magnetic field, the atomic moments are oriented in the direction of the magnetic field. However, the current directions in adjacent current loops being in opposite directions, there is no current within the volume of the material. However, the currents do not cancel at the surface of the substance on which there is a net current which gives rise to its own magnetic field.
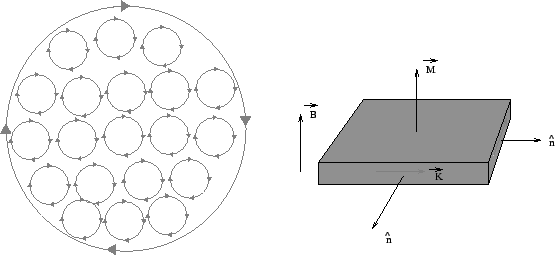
We define magnetization ![]() of a sample as the net magnetic moment per unit volume. The unit of magnetization is Ampere/meter. From the figure it can be seen that the surface current flows along the side faces. Denoting the normal to the face by
of a sample as the net magnetic moment per unit volume. The unit of magnetization is Ampere/meter. From the figure it can be seen that the surface current flows along the side faces. Denoting the normal to the face by ![]() , the surface current density
, the surface current density ![]() (in A/m) is given by
(in A/m) is given by