SKEDSOFT

Introduction: Six-sigma is an organized and systematic problem-solving method for strategic system improvement and new product and service development that relies on statistical methods and the scientific method to make dramatic reductions in customer defined defect rates and/or improvements in key output variables.

The Law of the Unconscious Statistician:

A result from integration theory broadens the applicability of expected value Monte Carlo. It is called the law of the unconscious statistician:

where f(x) is the distribution function the random variable x. Then, to calculate E[g(X)], we can generate IID g(X) using IID X from the distribution function f(x).

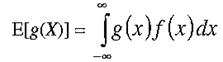
In this way, Monte Carlo simulation can evaluate a wide variety of expected values. For example, if g(X) is an “indicator function” which is a 1 if an event A occurs and 0 otherwise, then E[g(X)] = Pr{A}.

This law can be proven using some of the basic definitions associated with integrals. Intuitively, if the probability that {X = x} is proportional to f(x), the probability that {g(X) = g(x)} is also proportional to f(x).

Example  Estimate

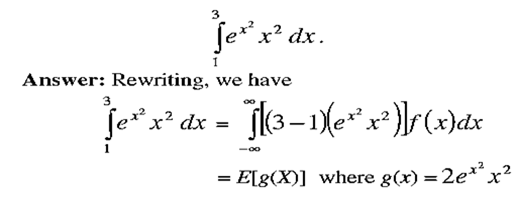
• and where f(x) is the density function for a uniform distribution with a = 1 and b = 3. Also, X ~ U[1,3], i.e., X is uniformly distributed with a = 1 and b = 3. Therefore, the pseudo-random U[0,1] numbers 0.23723063, 0.550678204, 0.873658577, 0.778915995, 0.383476144, 0.864940088, 0.636837027, 0.388494494, and 0.033923503 can be used to construct the pseudo-random sequence 1.474461, 2.101356, 2.747317, 2.557832, 1.766952, 2.72988, 2.273674,
• which pretend to be IID U[1,3]. Using the inverse cumulative is equivalent to multiplying by (b – a) and then adding a.
• From this sequence, one constructs the sequence 38.24, 730.71, 28628.23, 9081.29, 141.71, 25691.32, 1818.08, 148.51, and 7.13, which we pretend are IID samples of 2 2 2e X X . The average of these numbers is 7365.0 and the standard
• deviation is 11607. Therefore, the Monte Carlo estimate for the original integral is 7365.0 with estimated error 11607/3 = 3869.0. Using 10,000 pseudo-random numbers the estimate is 10949.51 with standard error 255.9. Therefore the true
• integral value is very likely within 768 of 10949.5 (three standard deviations or 3.0 × σ_estimate).