SKEDSOFT

NDTMs: An NDTM is a Turing machine with nondeterminism in its finite-state control, much like we have seen for earlier machine types such as PDAs. To motivate the incorporation of nondeterminism into Turing machines, consider a problem such as determining whether an undirected graph G has a clique (a completely connected subgraph) of k nodes.4 No efficient algorithm for this problem is known: all known algorithms have a worst-case exponential time complexity. Computer scientists have found that there exist thousands of problems such as this that arise in many practical contexts. They have not yet found a method to construct a polynomial algorithm for these problems. However, they have discovered another promising approach:

• They have found a way to formally define a class called “NPcomplete” such that finding a polynomial algorithm for even one of the problems in the NP-complete class will allow one to find a polynomial algorithm for all of the problems in the NP-complete class. Furthermore, most of these thousands of problems that have confounded scientists have been shown to belong to the NP-complete class.
• In short, scientists now have the strong hope of resorting to the maxim introduced in Chapter 1, namely: “solving one implies solving all,” meaning solving even one NP-complete problem using a polynomialtime algorithm will provide a polynomial-time algorithm for the thousands of known NP-complete problems.
• The aforesaid techniques rely on measuring the runtime of nondeterministic algorithms in a certain way which will be made precise in Chapter 20, but briefly consists of the following approach:
• If an NDTM can solve a certain problem P in polynomial-time, then the problem belongs to the class “NP.” If, in addition, problem P belongs to the “NP-hard” class, then this combination (being in NP and NP-hard) ensures that P is in the NP-complete class.

Guess and check: While all this may sound bizarre, the fundamental ideas are quite simple. The crux of the matter is that many problems can be solved by the “guess and check” approach. For instance, finding the prime factors of very large numbers is hard. As [98] summarizes, it was conjectured by Mersenne that 2⁶⁷ − 1 is prime. This conjecture remained open for two centuries until Frank Cole showed, in 1903, that it wasn’t; in fact, 2⁶⁷−1 = 193707721×761838257287. Therefore, if we could somehow have guessed that 193707721 and 761838257287 are the factors of 2⁶⁷ − 1, then checking the result would have been extremely easy! The
surprising thing is that there are two gradations of “difficulty” among problems for which only exponential algorithms seem to exist: those for which short guesses exist, and checking the guesses is easy, and those for which the existence of short guesses is, as yet, unknown.

To sum up:

• If, for a problem p, we can generate a “short guess” and check the guess efficiently, then p belongs to the class NP. Clique is in NP (as we will see in more detail in the next chapter) because a “guess” will be short (simply write out k of the graph nodes) and the “check” is easy (see if these nodes include a k-clique).
• If a problem is NP-complete, it is believed to be unlikely that it will have a polynomial algorithm, although this issue is open.
• Problems for which the guesses are not short, and also checking guesses is not easy, do not belong to NP. Hence, these problems are thought to be much harder to solve.

For instance, Clique is the problem: “the given graph does not have a k-clique.” There is no known way to produce a succinct guess of a solution for this problem, let alone check the guess efficiently. Every purported solution that a graph does not have a k-clique seems to warrant providing a guess of a solution of the form, “this set of k nodes does not span a clique; neither does this other set of k nodes; etc. etc.” This may, however, end up enumerating all k-node combinations, which are exponential in number.
NDTMs are machines that make the study of complexity theory in the above-listed manner possible. Their use in defining complexityclasses such as NP-hard and NP-complete forms the main hope for finding efficient algorithms for thousands of naturally occurring NPcomplete problems—or to prove that such algorithms cannot exist.

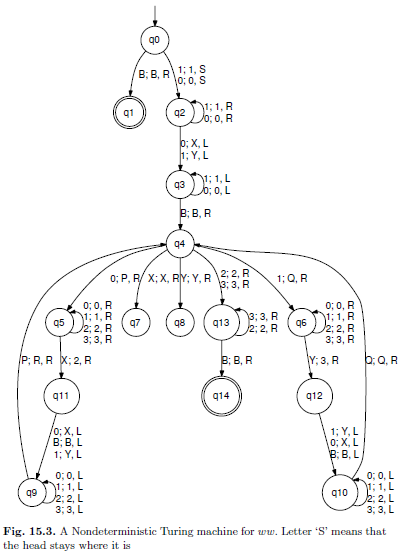
An NDTM for ww: In Figure 15.3, we provide a nondeterministic Turing machine for the language of strings of the form ww, where w ∈ Σ∗. Letter ‘S’ in the edge
from q0 to q2 means that the head stays where it is (can be simulated by an R followed by an L). This TM has to “guess” the midpoint; this happens in the initial nondeterministic loop situated at state q2. Notice that the Turing machine can stay in q2, skipping over the 0s and 1s or exit to state q3, replacing a 0 with an X or a 1 with a Y. This is how the Turing machine decides the midpoint; after this step, the Turing machine zigzags and tries to match and score off around the assumed midpoint. Any wrong guess causes this check phase to fail. One guess is guaranteed to win if, indeed, the input is of the form ww. The animation of this NDTM in action using JFLAP would be highly intuitive, and the reader is strongly urged to do so.