SKEDSOFT
Stability analysis using Nyquist stability criterion
If the Nyquist path in the s plane encircles Z zeros and P poles of 1 G(s)H(s) and does not pass through any poles or zeros of 1 G(s)H(s) as a representative point s moves in the clockwise direction along the Nyquist path, then the corresponding contour in the G(s)H(s) plane encircles the -1 j0 point N = Z - P times in the clockwise direction. (Negative values of N imply counterclockwise encirclements.)
In examining the stability of linear control systems using the Nyquist stability criterion, we see that three possibilities can occur.
1. There is no encirclement of the -1 j0 point. This implies that the system is stable if there are no poles of G(s)H(s) in the right-half s plane; otherwise, the system is unstable.
2. There is a counterclockwise encirclement or encirclements of the -1 j0 point. In this case the system is stable if the number of counterclockwise encirclements is the same as the number of poles G(s)H(s) in the right-half s plane; otherwise, the system is unstable.
3. There is a clockwise encirclement or encirclements of the -1 j0 point. In this case the system is unstable.
EXMAPLE:
Consider a closed loop system whose open-loop transfer function is given by
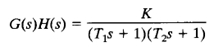
A plot of G(jω )H(jω) is shown in Figure1.
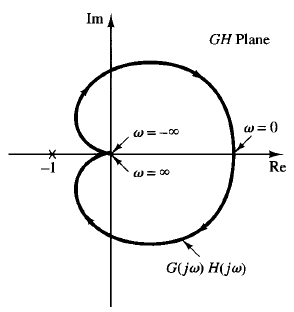
Fig: 1 Polar plot of G(jω )H(jω)
Since G(s)H(s) does not have any poles in the right-half s plane and the -1 j0 point is not encircled by the G(jω )H(jω) locus, this system is stable for any positive values of K, T1, and T2.