SKEDSOFT

Design Analysis Of Algorithm

Flow networks: In this section, a graph-theoretic definition of flow networks, discuss their properties, and define the maximum-flow problem precisely. We also introduce some helpful notation.

Flow networks and flows

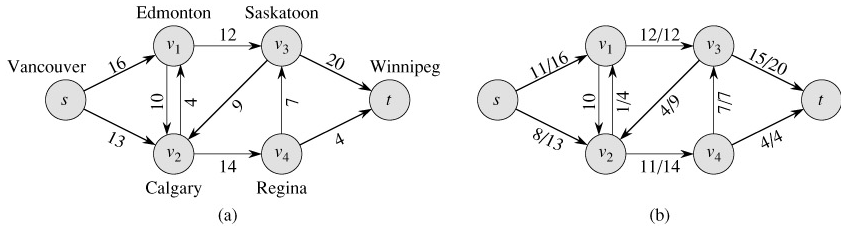
A flow network G = (V, E) is a directed graph in which each edge (u, v) ∈E has a nonnegative capacity c(u, v) ≥ 0. If (u, v) ∉ E, we assume that c(u, v) = 0. We distinguish two vertices in a flow network: a source s and a sink t. For convenience, we assume that every vertex lies on some path from the source to the sink. That is, for every vertex v ∈ V, there is a path 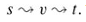The graph is therefore connected, and |E| ≥ |V | - 1. Figure 26.1 shows an example of a flow network.

We are now ready to define flows more formally. Let G = (V, E) be a flow network with a capacity function c. Let s be the source of the network, and let t be the sink. A flow in G is a real-valued function f : V × V → R that satisfies the following three properties:

Figure 26.1: (a) A flow network G = (V, E) for the Lucky Puck Company's trucking problem. The Vancouver factory is the source s, and the Winnipeg warehouse is the sink t. Pucks are shipped through intermediate cities, but only c(u, v) crates per day can go from city u to city v. Each edge is labeled with its capacity. (b) A flow f in G with value |f| = 19. Only positive flows are shown. If f (u, v) > 0, edge (u, v) is labeled by f(u, v)/c(u, v). (The slash notation is used merely to separate the flow and capacity; it does not indicate division.) If f(u, v) ≤ 0, edge (u, v) is labeled only by its capacity.

Capacity constraint: For all u, v ∈ V, we require f (u, v) ≤ c(u, v).

Skew symmetry: For all u, v ∈ V, we require f (u, v) = - f (v, u).

Flow conservation: For all u ∈ V - {s, t}, we require

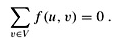
The quantity f (u, v), which can be positive, zero, or negative, is called the flow from vertex u to vertex v. The value of a flow f is defined as

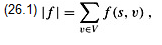
that is, the total flow out of the source. (Here, the |·| notation denotes flow value, not absolute value or cardinality.) In the maximum-flow problem, we are given a flow network G with source s and sink t, and we wish to find a flow of maximum value.

Before seeing an example of a network-flow problem, let us briefly explore the three flow properties. The capacity constraint simply says that the flow from one vertex to another must not exceed the given capacity. Skew symmetry is a notational convenience that says that the flow from a vertex u to a vertex v is the negative of the flow in the reverse direction. The flow-conservation property says that the total flow out of a vertex other than the source or sink is 0. By skew symmetry, we can rewrite the flow-conservation property as

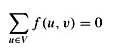
for all v ∈ V - {s, t}. That is, the total flow into a vertex is 0.

When neither (u, v) nor (v, u) is in E, there can be no flow between u and v, and f(u, v) = f(v, u) = 0. Our last observation concerning the flow properties deals with flows that are positive. The total positive flow entering a vertex v is defined by

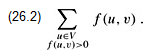
The total positive flow leaving a vertex is defined symmetrically. We define the total net flow at a vertex to be the total positive flow leaving a vertex minus the total positive flow entering a vertex. One interpretation of the flow-conservation property is that the total positive flow entering a vertex other than the source or sink must equal the total positive flow leaving that vertex. This property, that the total net flow at a vertex must equal 0, is often informally referred to as "flow in equals flow out."