SKEDSOFT
and we wish to solve for the unknown x. The LUP decomposition is
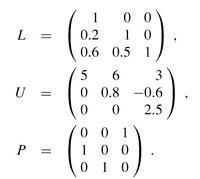
(The reader can verify that P A = LU.) Using forward substitution, we solve Ly = Pb for y:
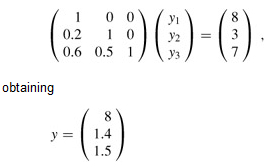
by computing first y1, then y2, and finally y3. Using back substitution, we solve U x = y for x:
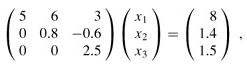
thereby obtaining the desired answer
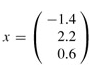
by computing first x3, then x2, and finally x1.
Computing an LU decomposition: We have now shown that if an LUP decomposition can be computed for a nonsingular matrix A, forward and back substitution can be used to solve the system Ax = b of linear equations. It remains to show how an LUP decomposition for A can be found efficiently. We start with the case in which A is an n × n nonsingular matrix and P is absent (or, equivalently, P = In). In this case, we must find a factorization A = LU . We call the two matrices L and U an LU decomposition of A.
The process by which we perform LU decomposition is called Gaussian elimination. We start by subtracting multiples of the first equation from the other equations so that the first variable is removed from those equations. Then, we subtract multiples of the second equation from the third and subsequent equations so that now the first and second variables are removed from them. We continue this process until the system that is left has an upper-triangular form-in fact, it is the matrix U. The matrix L is made up of the row multipliers that cause variables to be eliminated.
Our algorithm to implement this strategy is recursive. We wish to construct an LU decomposition for an n × n nonsingular matrix A. If n = 1, then we're done, since we can choose L = I1 and U = A. For n > 1, we break A into four parts:

where v is a size-(n - 1) column vector, wT is a size-(n - 1) row vector, and A′ is an (n - 1) × (n - 1) matrix. Then, using matrix algebra (verify the equations by simply multiplying through), we can factor A as
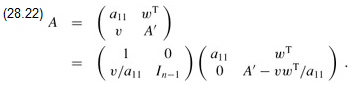
The 0's in the first and second matrices of the factorization are row and column vectors, respectively, of size n - 1. The term vwT/a11, formed by taking the outer product of v and w and dividing each element of the result by a11, is an (n - 1) × (n - 1) matrix, which conforms in size to the matrix A′ from which it is subtracted. The resulting (n - 1) × (n - 1) matrix
![]() is called the Schur complement of A with respect to a11.
is called the Schur complement of A with respect to a11.