SKEDSOFT

Design Analysis Of Algorithm

String matching with finite automata

Many string-matching algorithms build a finite automaton that scans the text string T for all occurrences of the pattern P. This section presents a method for building such an automaton. These string-matching automata are very efficient: they examine each text character exactly once, taking constant time per text character. The matching time used-after preprocessing the pattern to build the automaton-is therefore Θ(n). The time to build the automaton, however, can be large if Σ is large. Section 32.4 describes a clever way around this problem.

We begin this section with the definition of a finite automaton. We then examine a special string-matching automaton and show how it can be used to find occurrences of a pattern in a text. This discussion includes details on how to simulate the behavior of a string-matching automaton on a given text. Finally, we shall show how to construct the string-matching automaton for a given input pattern.

Finite automata

A finite automaton M is a 5-tuple (Q, q0, A, Σ, δ), where

  • Q is a finite set of states,

  • q0 ∈ Q is the start state,

  • A ⊆ Q is a distinguished set of accepting states,

  • Σ is a finite input alphabet,

  • δ is a function from Q × Σ into Q, called the transition function of M.

The finite automaton begins in state q0 and reads the characters of its input string one at a time. If the automaton is in state q and reads input character a, it moves ("makes a transition") from state q to state δ(q, a). Whenever its current state q is a member of A, the machine M is said to have accepted the string read so far. An input that is not accepted is said to be rejected. Figure 32.6 illustrates these definitions with a simple two-state automaton.

Figure 32.6: A simple two-state finite automaton with state set Q = {0, 1}, start state q0 = 0, and input alphabet Σ = {a, b}. (a) A tabular representation of the transition function δ. (b) An equivalent state-transition diagram. State 1 is the only accepting state (shown blackened). Directed edges represent transitions. For example, the edge from state 1 to state 0 labeled b indicates δ(1, b) = 0. This automaton accepts those strings that end in an odd number of a's. More precisely, a string x is accepted if and only if x = yz, where y = ε or y ends with a b, and z = ak, where k is odd. For example, the sequence of states this automaton enters for input abaaa (including the start state) is 〈0, 1, 0, 1, 0, 1〉, and so it accepts this input. For input abbaa, the sequence of states is 〈0, 1, 0, 0, 1, 0〉, and so it rejects this input.

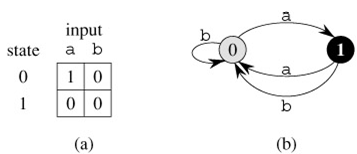
A finite automaton M induces a function φ, called the final-state function, from Σ* to Q such that φ(w) is the state M ends up in after scanning the string w. Thus, M accepts a string w if and only if φ(w) ∈ A. The function φ is defined by the recursive relation

φ(ε)

=

q0,

φ(wa)

=

δ(φ(w), a) for w ∈ Σ*, a ∈ Σ.

String-matching automata

There is a string-matching automaton for every pattern P; this automaton must be constructed from the pattern in a preprocessing step before it can be used to search the text string. Figure 32.7 illustrates this construction for the pattern P = ababaca. From now on, we shall assume that P is a given fixed patternstring; for brevity, we shall not indicate the dependence upon P in our notation.

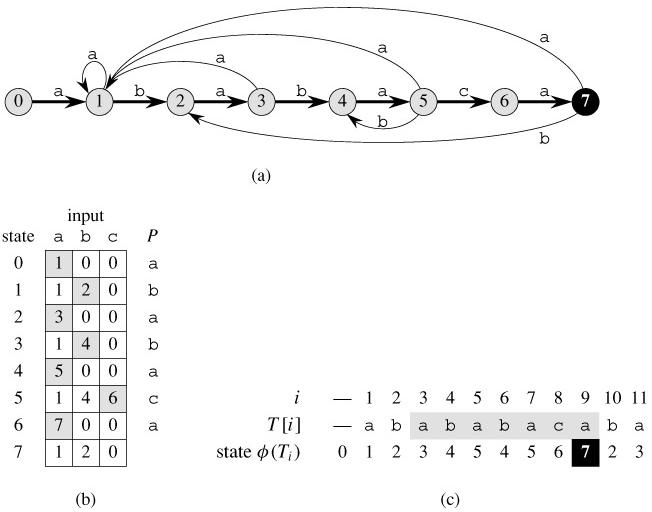Figure 32.7: (a) A state-transition diagram for the string-matching automaton that accepts all strings ending in the string ababaca. State 0 is the start state, and state 7 (shown blackened) is the only accepting state. A directed edge from state i to state j labeled a represents δ(i, a) = j. The right-going edges forming the "spine" of the automaton, shown heavy in the figure, correspond to successful matches between pattern and input characters. The left-going edges correspond to failing matches. Some edges corresponding to failing matches are not shown; by convention, if a state i has no outgoing edge labeled a for some a ∈ Σ, then δ(i, a) = 0. (b) The corresponding transition function δ, and the pattern string P = ababaca. The entries corresponding to successful matches between pattern and input characters are shown shaded. (c) The operation of the automaton on the text T = abababacaba. Under each text character T [i] is given the state φ(Ti) the automaton is in after processing the prefix Ti. One occurrence of the pattern is found, ending in position 9.