SKEDSOFT

Design Analysis Of Algorithm

Lemma 30.6: (Summation lemma)

For any integer n ≥ 1 and nonnegative integer k not divisible by n,

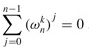
Proof Equation (A.5) applies to complex values as well as to reals, and so we have

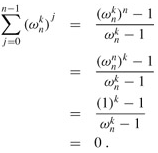
Requiring that k not be divisible by n ensures that the denominator is not 0, since 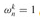only when k is divisible by n.

The DFT: Recall that we wish to evaluate a polynomial

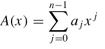
of degree-bound n at 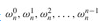(that is, at the n complex nth roots of unity).Without loss of generality, we assume that n is a power of 2, since a given degree-bound can always be raised -we can always add new high-order zero coefficients as necessary.We assume that A is given in coefficient form: a = (a0, a1,..., an-1). Let us define the results yk, for k = 0, 1,..., n - 1, by

(30.8) 

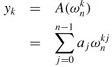The vector y = (y0, y1,..., yn-1) is the Discrete Fourier Transform (DFT) of the coefficient vector a = (a0, a1,..., an-1). We also write y = DFTn(a).

The FFT

By using a method known as the Fast Fourier Transform (FFT), which takes advantage of the special properties of the complex roots of unity, we can compute DFTn(a)in time Θ(n lg n), as opposed to the Θ(n2) time of the straightforward method.

The FFT method employs a divide-and-conquer strategy, using the even-index and odd-index coefficients of A(x) separately to define the two new polynomials A[0](x) and A[1](x) of degree-bound n/2:

A[0](x) = a0 a2x a4x2 ··· an-2xn/2-1,

A[1](x) = a1 a3x a5x2 ··· an-1xn/2-1.

Note that A[0] contains all the even-index coefficients of A (the binary representation of the index ends in 0) and A[1] contains all the odd-index coefficients (the binary representation of the index ends in 1). It follows that

(30.9) 

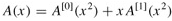so that the problem of evaluating A(x) at reduces to

  1. evaluating the degree-bound n/2 polynomials A[0](x) and A[1](x) at the points

    (30.10)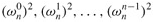 

    and then

  2. combining the results according to equation (30.9).